Okrąg Apoloniusza»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: XXXVI OM
- Zadanie pochodzi z artykułu Okrąg Apoloniusza
- Publikacja w Delcie: styczeń 2013
- Publikacja elektroniczna: 01-01-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Punkty
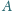 i
i
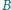 nie należą do płaszczyzny
nie należą do płaszczyzny
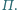 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
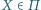 o tej własności, że proste
o tej własności, że proste
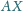 i
i
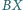 tworzą z płaszczyzną
tworzą z płaszczyzną
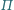 równe kąty.
równe kąty.

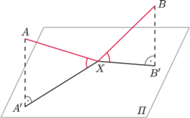
 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
 na
płaszczyznę
na
płaszczyznę
 Dla punktu
Dla punktu
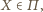 różnego od
różnego od
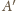 i
i
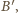 równość
równość
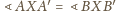 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
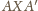 i
i
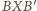 są podobne.
Równoważnie,
są podobne.
Równoważnie,
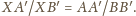 Jeśli
Jeśli
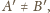 to
punkty
to
punkty
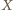 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
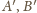 i stałej
i stałej
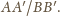 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
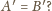 Czy możliwe, by
Czy możliwe, by