Okrąg Apoloniusza»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Okrąg Apoloniusza
- Publikacja w Delcie: styczeń 2013
- Publikacja elektroniczna: 01-01-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
W przestrzeni dane są różne punkty
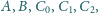przy czym
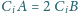dla
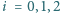oraz
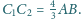Udowodnij,
że kąt
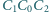jest prosty i że punkty
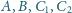leżą na jednej
płaszczyźnie.
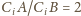dla
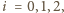więc wszystkie punkty
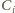leżą na sferze Apoloniusza dla punktów
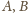i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
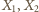na prostej
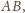spełniające warunek
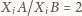dla
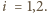Wówczas
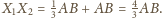
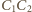także jest średnicą rozważanej sfery. Stąd
kąt
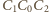jest prosty, jako wpisany oparty na średnicy. Proste
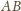i
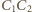przecinają się (w środku sfery), więc punkty
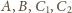leżą na jednej płaszczyźnie.