Nie można.
Wystarczy, jeśli znajdziemy dwa czworościany o różnych
objętościach, dla których wspomniane 5 wielkości są jednakowe. Dobrym
pomysłem jest ograniczenie się do klasy czworościanów równościennych,
bowiem dla nich promień każdej ze sfer dopisanych jest 2 razy większy od
promienia sfery wpisanej. Wówczas dane 5 wielkości redukuje się do
jednej.
Teraz można by użyć wzorów na odpowiednie wielkości dla czworościanów
równościennych, ale prowadzi to do zawiłych rachunków. Znacznie
lepiej przeprowadzić następujące rozumowanie. Rozważmy sześcian
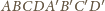 o krawędzi długości
o krawędzi długości
 i sferę dopisaną do
czworościanu równościennego
i sferę dopisaną do
czworościanu równościennego
 (a nawet foremnego) o
środku w punkcie
(a nawet foremnego) o
środku w punkcie
 . Oczywiście objętość czworościanu
. Oczywiście objętość czworościanu
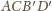 jest równa
jest równa
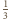 . Nietrudno też wyliczyć (np. wyrażając
objętość czworościanu
. Nietrudno też wyliczyć (np. wyrażając
objętość czworościanu
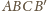 na dwa sposoby), że promień tej sfery
jest równy
na dwa sposoby), że promień tej sfery
jest równy
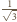 . Poprowadźmy teraz pewną płaszczyznę styczną do tej
sfery, która przecina półprostą
. Poprowadźmy teraz pewną płaszczyznę styczną do tej
sfery, która przecina półprostą
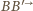 w pewnym punkcie
w pewnym punkcie
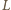 , który
leży bardzo daleko, zaś krawędzie
, który
leży bardzo daleko, zaś krawędzie
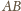 i
i
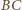 w punktach
w punktach
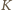 i
i
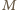 . Niech
. Niech
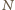 będzie punktem na płaszczyźnie
będzie punktem na płaszczyźnie
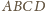 takim, że czworokąt
takim, że czworokąt
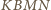 jest prostokątem, zaś
jest prostokątem, zaś
 ,
,
 ,
,
 takimi punktami, że wielościan
takimi punktami, że wielościan
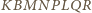 jest
prostopadłościanem. Zauważmy, że długości odcinków
jest
prostopadłościanem. Zauważmy, że długości odcinków
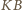 i
i
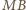 są ograniczone z dołu przez promień sfery o środku w
są ograniczone z dołu przez promień sfery o środku w
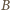 ,
czyli
,
czyli
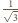 , zaś odcinek
, zaś odcinek
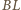 może być dowolnie duży. Wynika
stąd, że objętość prostopadłościanu
może być dowolnie duży. Wynika
stąd, że objętość prostopadłościanu
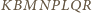 moze być
dowolnie duża. To samo można powiedzieć o objętości czworościanu
równościennego
moze być
dowolnie duża. To samo można powiedzieć o objętości czworościanu
równościennego
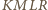 wpisanego w ten prostopadłościan. Jednakże
promień sfery dopisanej do niego o środku w
wpisanego w ten prostopadłościan. Jednakże
promień sfery dopisanej do niego o środku w
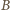 jest równy
jest równy
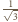 ,
tyle samo wynoszą promienie pozostałych sfer dopisanych, zaś promień sfery
wpisanej jest 2 razy mniejszy. Znaleźliśmy więc dwa czworościany
równościenne, które mają sfery wpisane o jednakowych promieniach,
jak i sfery dopisane o równych promieniach; a jednak ich objętości są
różne.
,
tyle samo wynoszą promienie pozostałych sfer dopisanych, zaś promień sfery
wpisanej jest 2 razy mniejszy. Znaleźliśmy więc dwa czworościany
równościenne, które mają sfery wpisane o jednakowych promieniach,
jak i sfery dopisane o równych promieniach; a jednak ich objętości są
różne.

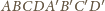 o krawędzi długości
o krawędzi długości
 i sferę dopisaną do
czworościanu równościennego
i sferę dopisaną do
czworościanu równościennego
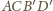 (a nawet foremnego) o
środku w punkcie
(a nawet foremnego) o
środku w punkcie
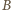 . Oczywiście objętość czworościanu
. Oczywiście objętość czworościanu
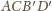 jest równa
jest równa
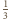 . Nietrudno też wyliczyć (np. wyrażając
objętość czworościanu
. Nietrudno też wyliczyć (np. wyrażając
objętość czworościanu
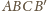 na dwa sposoby), że promień tej sfery
jest równy
na dwa sposoby), że promień tej sfery
jest równy
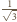 . Poprowadźmy teraz pewną płaszczyznę styczną do tej
sfery, która przecina półprostą
. Poprowadźmy teraz pewną płaszczyznę styczną do tej
sfery, która przecina półprostą
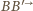 w pewnym punkcie
w pewnym punkcie
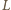 , który
leży bardzo daleko, zaś krawędzie
, który
leży bardzo daleko, zaś krawędzie
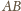 i
i
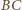 w punktach
w punktach
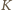 i
i
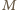 . Niech
. Niech
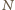 będzie punktem na płaszczyźnie
będzie punktem na płaszczyźnie
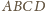 takim, że czworokąt
takim, że czworokąt
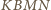 jest prostokątem, zaś
jest prostokątem, zaś
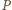 ,
,
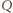 ,
,
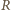 takimi punktami, że wielościan
takimi punktami, że wielościan
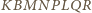 jest
prostopadłościanem. Zauważmy, że długości odcinków
jest
prostopadłościanem. Zauważmy, że długości odcinków
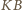 i
i
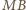 są ograniczone z dołu przez promień sfery o środku w
są ograniczone z dołu przez promień sfery o środku w
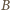 ,
czyli
,
czyli
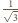 , zaś odcinek
, zaś odcinek
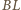 może być dowolnie duży. Wynika
stąd, że objętość prostopadłościanu
może być dowolnie duży. Wynika
stąd, że objętość prostopadłościanu
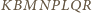 moze być
dowolnie duża. To samo można powiedzieć o objętości czworościanu
równościennego
moze być
dowolnie duża. To samo można powiedzieć o objętości czworościanu
równościennego
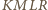 wpisanego w ten prostopadłościan. Jednakże
promień sfery dopisanej do niego o środku w
wpisanego w ten prostopadłościan. Jednakże
promień sfery dopisanej do niego o środku w
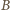 jest równy
jest równy
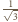 ,
tyle samo wynoszą promienie pozostałych sfer dopisanych, zaś promień sfery
wpisanej jest 2 razy mniejszy. Znaleźliśmy więc dwa czworościany
równościenne, które mają sfery wpisane o jednakowych promieniach,
jak i sfery dopisane o równych promieniach; a jednak ich objętości są
różne.
,
tyle samo wynoszą promienie pozostałych sfer dopisanych, zaś promień sfery
wpisanej jest 2 razy mniejszy. Znaleźliśmy więc dwa czworościany
równościenne, które mają sfery wpisane o jednakowych promieniach,
jak i sfery dopisane o równych promieniach; a jednak ich objętości są
różne.
 jest promieniem okręgu wpisanego w pewien
trójkąt, zaś
jest promieniem okręgu wpisanego w pewien
trójkąt, zaś
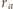 ,
,
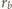 i
i
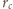 promieniami okręgów do niego
dopisanych, to pole tego trójkąta jest równe
promieniami okręgów do niego
dopisanych, to pole tego trójkąta jest równe
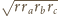 .
.