Czworościany równościenne - część II»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Czworościany równościenne - część II
- Publikacja w Delcie: październik 2012
- Publikacja elektroniczna: 30-09-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)
Dany jest czworościan
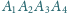 . Przez
. Przez
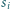 oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
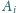 i kuli wpisanej w ten czworościan. Wiadomo, że
i kuli wpisanej w ten czworościan. Wiadomo, że
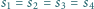 . Rozstrzygnąć, czy czworościan ten musi być
foremny.
. Rozstrzygnąć, czy czworościan ten musi być
foremny.

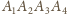 będzie dowolnym nieforemnym czworościanem
równościennym. Ponieważ odcinek łączący środki krawędzi
będzie dowolnym nieforemnym czworościanem
równościennym. Ponieważ odcinek łączący środki krawędzi
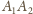 i
i
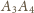 jest do nich prostopadły, to przekształcenie będące obrotem wokół
tego odcinka o
jest do nich prostopadły, to przekształcenie będące obrotem wokół
tego odcinka o
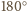 przeprowadza dany czworościan na siebie. W
szczególności kula wpisana w ten czworościan również musi przejść na
siebie. Przy tym przekształceniu punkt
przeprowadza dany czworościan na siebie. W
szczególności kula wpisana w ten czworościan również musi przejść na
siebie. Przy tym przekształceniu punkt
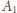 przechodzi na
przechodzi na
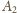 zaś
zaś
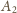 na
na
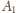 i podobnie
i podobnie
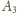 przechodzi na
przechodzi na
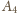 i
na odwrót. W takim razie środkowa poprowadzona z wierzchołka
i
na odwrót. W takim razie środkowa poprowadzona z wierzchołka
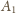 przechodzi na środkową poprowadzoną z wierzchołka
przechodzi na środkową poprowadzoną z wierzchołka
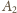 .
Skoro jednak kula wpisana jest zachowywana, to część wspólna jednej
środkowej z kulą przechodzi na część wspólną drugiej środkowej z tą
kulą. To oznacza, że
.
Skoro jednak kula wpisana jest zachowywana, to część wspólna jednej
środkowej z kulą przechodzi na część wspólną drugiej środkowej z tą
kulą. To oznacza, że
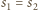 . Podobnie udowodnimy pozostałe
równości.
. Podobnie udowodnimy pozostałe
równości.