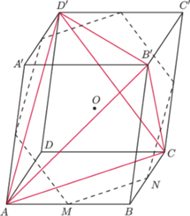
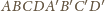Niech  będzie równoległościanem 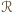 rozważanym w zadaniu. Jak wiemy z poprzedniego odcinka, wystarczy, jeśli wykażemy, że czworościan 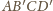 wpisany w ten równoległościan jest równościenny, a to będzie udowodnione, gdy uzasadnimy, że pola jego ścian są równe.

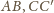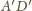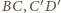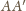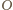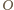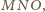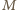Rozważmy przekrój płaszczyzną przechodzącą przez środki krawędzi  i   (rysunek). Nietrudno udowodnić, że przekrój ten jest sześciokątem przechodzącym także przez środki krawędzi  i   oraz zawierającym środek symetrii  danego równoległościanu. Punkt  jest także środkiem symetrii tego sześciokąta, więc pole rozważanego przekroju jest 6 razy większe niż pole trójkąta  gdzie  i 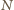 są środkami odcinków 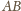 i 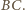  Z drugiej strony pole tego trójkąta jest 4 razy mniejsze niż pole trójkąta 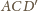 będącego ścianą czworościanu 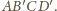 Stąd wniosek, że pole ściany 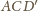 stanowi 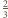 pola rozważanego przekroju.

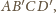Ponieważ podobne rozumowanie można przeprowadzić dla pozostałych ścian czworościanu  to z równości pól danych przekrojów wynika równość pól ścian tego czworościanu – a to właśnie chcieliśmy wykazać.