Kąty dwuścienne»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: Olimpiada Matematyczna IMO LONGLIST 1986
- Zadanie pochodzi z artykułu Kąty dwuścienne
- Publikacja w Delcie: październik 2011
- Publikacja elektroniczna: 02-10-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (64 KB)
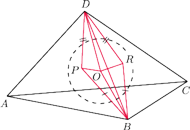
Punkt
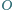 jest środkiem sfery wpisanej w czworościan
jest środkiem sfery wpisanej w czworościan
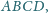 przy czym prosta
przy czym prosta
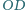 jest prostopadła do krawędzi
jest prostopadła do krawędzi
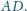 Znaleźć miarę kąta dwuściennego między płaszczyznami
Znaleźć miarę kąta dwuściennego między płaszczyznami
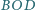 i
i
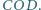

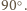 Niech
Niech
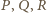 będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
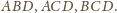 Z równości
Z równości
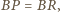
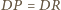 i
i
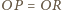 wnioskujemy, że czworościany
wnioskujemy, że czworościany
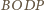 i
i
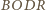 są przystające (
są przystające (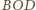 i
i
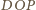 jest równy kątowi dwuściennemu
między płaszczyznami
jest równy kątowi dwuściennemu
między płaszczyznami
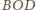 i
i
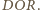 Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
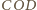 i
i
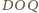 jest
równy kątowi dwuściennemu między płaszczyznami
jest
równy kątowi dwuściennemu między płaszczyznami
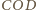 i
i
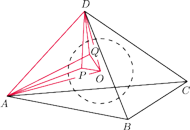
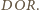 Wykażemy, że punkty
Wykażemy, że punkty
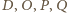 leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
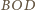 i
i
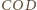 ma miarę
ma miarę
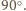
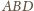 jest prostopadła do prostej
jest prostopadła do prostej
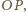 to
to
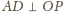 (
(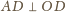 dostajemy
dostajemy
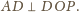 Analogicznie udowodnimy, że
Analogicznie udowodnimy, że
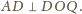 Zatem punkty
Zatem punkty
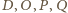 leżą na jednej
płaszczyźnie prostopadłej do krawędzi
leżą na jednej
płaszczyźnie prostopadłej do krawędzi
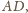 co kończy dowód.
co kończy dowód.