Kąty płaskie w przestrzeni»Zadanie 9
o zadaniu...
- Zadanie olimpijskie: OM 35-I-12
- Zadanie pochodzi z artykułu Kąty płaskie w przestrzeni
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (53 KB)
W kącie trójściennym
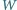 zawarta jest półprosta
zawarta jest półprosta
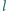 przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
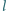 z krawędziami kąta
z krawędziami kąta
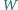 nie przekracza sumy kątów płaskich kąta
nie przekracza sumy kątów płaskich kąta
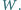

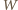 jest wierzchołkiem danego kąta trójściennego,
jest wierzchołkiem danego kąta trójściennego,
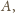
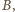
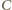 – dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
– dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
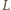 dowolnym punktem na półprostej
dowolnym punktem na półprostej
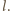 Mamy udowodnić, że
Mamy udowodnić, że
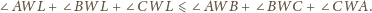
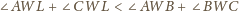
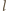 pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.
pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.