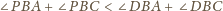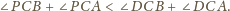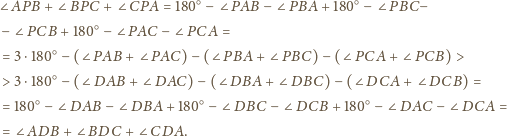Kąty płaskie w przestrzeni»Zadanie 8
o zadaniu...
- Zadanie olimpijskie: YUG 1985
- Zadanie pochodzi z artykułu Kąty płaskie w przestrzeni
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (53 KB)
Niech
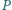 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
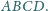 Dowieść, że
Dowieść, że


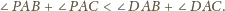
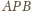 przecina krawędź
przecina krawędź
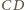 w
punkcie
w
punkcie
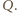 Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
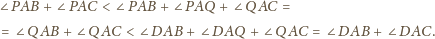
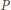 leży wewnątrz trójkąta
leży wewnątrz trójkąta
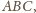 to
to
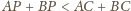 –
wystarczy rozważyć sferę o środku
–
wystarczy rozważyć sferę o środku
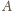 i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że