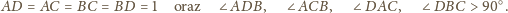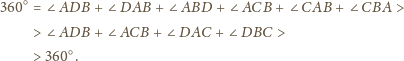Kąty płaskie w przestrzeni»Zadanie 7
o zadaniu...
- Zadanie olimpijskie: 53-II-5
- Zadanie pochodzi z artykułu Kąty płaskie w przestrzeni
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (53 KB)
Niech
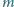 będzie liczbą krawędzi czworościanu o długości
będzie liczbą krawędzi czworościanu o długości
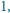 a
a
 liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
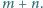

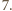
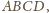 w którym
w którym
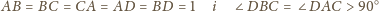
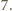 Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
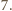 Wynika stąd w szczególności, że liczba krawędzi
długości
Wynika stąd w szczególności, że liczba krawędzi
długości
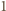 jest równa co najmniej
jest równa co najmniej
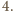 Jeśli jest
Jeśli jest
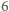 krawędzi
długości
krawędzi
długości
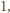 to nie ma kątów rozwartych. Jeśli jest
to nie ma kątów rozwartych. Jeśli jest
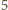 krawędzi
długości
krawędzi
długości
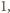 to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
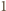 musi być równa
musi być równa
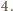 Tym samym
liczba kątów rozwartych musi być równa
Tym samym
liczba kątów rozwartych musi być równa
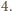 Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację: