Twierdzenie Menelaosa»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Twierdzenie Menelaosa
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
Sfera
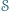 jest styczna do krawędzi
jest styczna do krawędzi
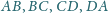 czworościanu
czworościanu
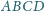 dpowiednio w punktach
dpowiednio w punktach
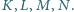 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.

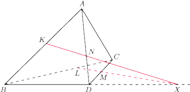
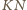 przecina prostą
przecina prostą
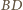 w pewnym punkcie
w pewnym punkcie
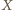 (poza odcinkiem
(poza odcinkiem
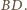 Wtedy z twierdzenia Menelaosa dla
trójkąta
Wtedy z twierdzenia Menelaosa dla
trójkąta
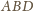 i prostej
i prostej
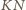 mamy
mamy
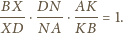
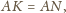
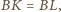
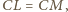
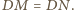 Wobec powyższego
Wobec powyższego
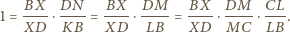
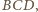 prosta
prosta
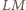 przecina prostą
przecina prostą
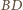 w punkcie
w punkcie
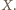 Stąd proste
Stąd proste
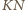 i
i
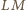 przecinają się, więc punkty
przecinają się, więc punkty
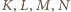 leżą na jednej
płaszczyźnie. Prostszy przypadek
leżą na jednej
płaszczyźnie. Prostszy przypadek
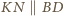 pozostawiam jako
ćwiczenie.
pozostawiam jako
ćwiczenie.