Klub 44M - zadania XI 2018»Zadanie 769
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2018
- Publikacja w Delcie: listopad 2018
- Publikacja elektroniczna: 31 października 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (75 KB)
W trapezie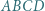 
o równoległych podstawach 
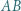i 
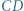zachodzą równości: 
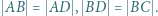Okrąg opisany na trójkącie 
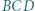przecina przekątną 
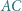w punkcie 
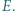Dowieść, że prosta 
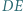połowi bok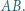 
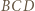jest równoramienny; symetralna boku 
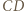jest osią symetrii tego trójkąta, więc i okręgu na nim opisanego; prosta 
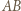(równoległa do 
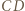) jest styczna do tego okręgu. Skoro 
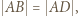zatem prosta 
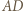też jest styczna. Wynikają stąd równości kątów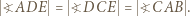
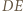przecina 
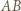w punkcie, który nazwiemy 
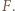Niech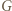 
będzie punktem symetrycznym do 
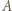względem 
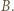Widzimy trapez równoramienny 
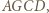z równymi kątami: 
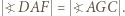Stąd i z wcześniejszej równości (przepisanej jako 
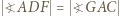) wynika podobieństwo trójkątów 
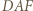i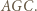 
W konsekwencji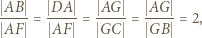
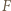jest środkiem odcinka 