Klub 44M - zadania X 2018»Zadanie 767
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2018
- Publikacja w Delcie: październik 2018
- Publikacja elektroniczna: 1 października 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (93 KB)
Kwadrat o boku długości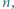 
będącej liczbą naturalną, został podzielony prostymi poziomymi i pionowymi na 
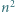kwadracików jednostkowych. Powstała siatka, utworzona z 
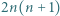odcinków jednostkowych (boków tych kwadracików). Używając czterech barw, należy te odcinki pokolorować (każdy odcinek jednym kolorem) tak, żeby każdy kwadracik jednostkowy miał boki różnych kolorów oraz by każdy bok dużego kwadratu uzyskał jednolity kolor - ale każdy inny. Dla jakich liczb naturalnych 
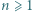jest to wykonalne?
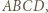prostopadłe do nich i przebiegające przez punkty kratowe. Gdy długość boku jest liczbą nieparzystą, żądane pokolorowanie da się banalnie wykonać: malujemy każdą linię (w całości) pojedynczym kolorem; linie równoległe do 
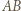naprzemiennie, dwoma kolorami; linie równoległe do 
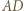też naprzemiennie, dwoma pozostałymi kolorami.
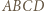będzie, jak poprzednio, kwadratem o boku długości nieparzystej, z pokolorowaniem opisanym powyżej. Przedłużamy jego boki 
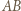i 
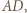każdy o jednostkę, otrzymując odcink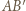i 
i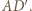 
Niech punkt 
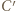dopełnia kwadrat 
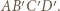Poprzednie pokolorowanie odcinków 
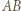i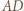 
przedłużamy na całe linie 
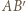i 
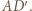Bok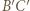 
malujemy kolorem odcinka 
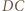; bok 
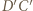malujemy kolorem odcinka 
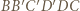sposób malowania odcinków jednostkowych, równoległych do 
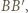jest już wymuszony przez postawione warunki - zaczynamy od 
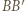(który już ma kolor) i malujemy kolejne równoległe odcinki, kończąc na tym, który ma jeden koniec w punkcie 
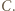Podobnie postępujemy z odcinkami jednostkowymi, równoległymi do 
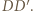Dzięki założeniu o nieparzystości długośc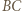i 
i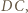 
kwadracik o wierzchołkach 
i 
będzie miał brzeg czterobarwny.