Klub 44M - zadania V 2018»Zadanie 761
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2018
- Publikacja w Delcie: maj 2018
- Publikacja elektroniczna: 30 kwietnia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (54 KB)
Trójkąt 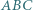 (nie prostokątny) jest wpisany w okrąg o średnicy
(nie prostokątny) jest wpisany w okrąg o średnicy 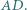 Punkt
Punkt 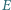 jest symetryczny do
jest symetryczny do 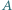 względem środka boku
względem środka boku 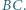 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 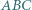 i
i 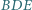 mają równe promienie.
mają równe promienie.

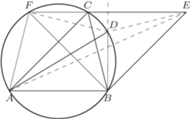
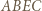 jest równoległobokiem. Niech prosta
jest równoległobokiem. Niech prosta 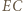 przecina okrąg, opisany na trójkącie
przecina okrąg, opisany na trójkącie 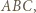 w punktach
w punktach 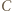 i
i 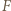 (gdy jest styczna, przyjmujemy
(gdy jest styczna, przyjmujemy 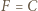 ). Powstaje trapez równoramienny
). Powstaje trapez równoramienny 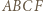 lub
lub 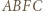 (gdy
(gdy 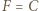 - trójkąt równoramienny). W każdym przypadku
- trójkąt równoramienny). W każdym przypadku 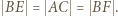
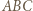 z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą
z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą 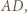 na której oparty jest kąt prosty
na której oparty jest kąt prosty 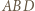 ; a ponieważ
; a ponieważ 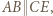 zatem
zatem 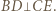 To znaczy, że w trójkącie równoramiennym
To znaczy, że w trójkącie równoramiennym 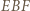 prosta
prosta 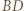 jest symetralną boku
jest symetralną boku 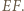 W konsekwencji trójkąt
W konsekwencji trójkąt 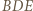 jest względem niej symetryczny do trójkąta
jest względem niej symetryczny do trójkąta 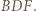 Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie
Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie