Pasujemy do siebie!»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: LV Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Pasujemy do siebie!
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (57 KB)
W sześciokącie wypukłym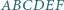 
wszystkie boki są równej długości oraz 
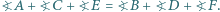Udowodnij, że przekątne 
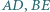i 
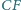przecinają się w jednym punkcie.
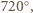więc z założenia wnioskujemy, że 
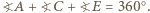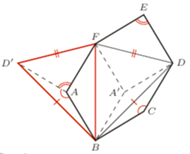
Stąd i z równości wszystkich boków sześciokąta wynika, że z trójkątów równoramiennych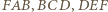 
można złożyć trójkąt 
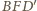w sposób przedstawiony na rysunku.
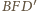i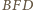 
są przystające (gdyż mają równe odpowiednie boki) oraz symetryczne względem prostej 
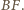Niech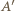 
będzie obrazem punktu 
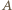w tej symetrii. Wówczas odcinki 
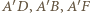mają długości równe bokom sześciokąta.
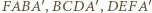są rombami, a więc 
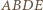jest równoległobokiem (bo odcink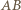i 
i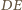 
są równe i równoległe). Wobec tego przekątne 
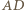i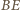 
mają wspólny środek. Analogicznie przekątne 
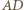i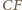 
mają wspólny środek, co kończy dowód.