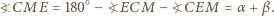Pasujemy do siebie!»Zadanie 3
o zadaniu...
- Zadanie olimpijskie: LVIII Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Pasujemy do siebie!
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (57 KB)
Dany jest pięciokąt wypukły 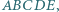 w którym
w którym 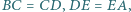
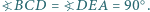 Udowodnij, że z odcinków o długościach
Udowodnij, że z odcinków o długościach 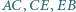 można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę
można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę  kąta
kąta 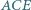 i miarę
i miarę 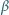 kąta
kąta 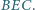

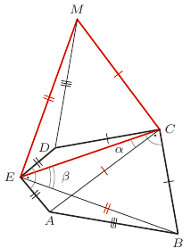
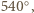 więc z założenia wnioskujemy, że w rozważanym pięciokącie
więc z założenia wnioskujemy, że w rozważanym pięciokącie 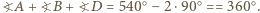 Stąd i z danych równości boków wynika, że z trójkątów
Stąd i z danych równości boków wynika, że z trójkątów  i
i 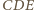 można złożyć trójkąt
można złożyć trójkąt 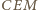 tak jak na rysunku, o bokach żądanej długości:
tak jak na rysunku, o bokach żądanej długości: 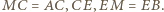
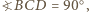 to także
to także 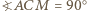 (gdyż kąty
(gdyż kąty 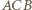 i
i 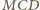 są przystające), a więc
są przystające), a więc 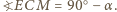 Analogicznie
Analogicznie 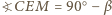 i wobec tego
i wobec tego