Klub 44M - zadania I 2018»Zadanie 753
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2018
- Publikacja w Delcie: styczeń 2018
- Publikacja elektroniczna: 1 stycznia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (102 KB)
Wewnątrz trójkąta 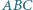 leży punkt
leży punkt 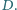 Proste
Proste 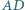 i
i 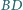 przecinają boki
przecinają boki 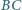 i
i 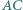 odpowiednio w punktach
odpowiednio w punktach 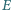 i
i 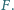 Udowodnić, że jeśli
Udowodnić, że jeśli 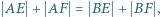 to
to 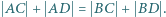

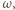 dopisany do trójkąta
dopisany do trójkąta 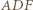 przy boku
przy boku 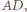 styczny do tego boku w punkcie
styczny do tego boku w punkcie 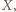 oraz okrąg
oraz okrąg 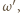 dopisany do trójkąta
dopisany do trójkąta 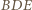 przy boku
przy boku 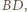 styczny do prostej
styczny do prostej 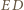 w punkcie
w punkcie 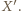 Wzory, wyrażające długości odcinków stycznych, są dobrze znane (lub/oraz łatwe do uzasadnienia):
Wzory, wyrażające długości odcinków stycznych, są dobrze znane (lub/oraz łatwe do uzasadnienia):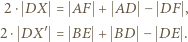
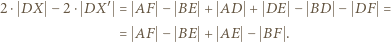
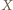 i
i 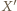 pokrywają się; to zaś oznacza, że
pokrywają się; to zaś oznacza, że 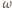 i
i 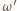 to ten sam okrąg, styczny do prostych
to ten sam okrąg, styczny do prostych 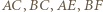 (kolejno) w punktach
(kolejno) w punktach 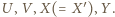 Z położenia tych punktów na odpowiednich prostych wynikają równości
Z położenia tych punktów na odpowiednich prostych wynikają równości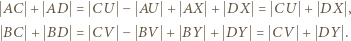
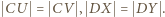 Stąd równość sum po lewych stronach - czyli teza zadania.
Stąd równość sum po lewych stronach - czyli teza zadania.