Klub 44M - zadania XI 2017»Zadanie 749
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2017
- Publikacja w Delcie: listopad 2017
- Publikacja elektroniczna: 31 października 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (66 KB)
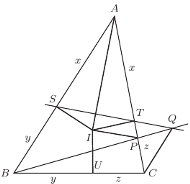
Trójkąt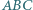 
jest opisany na okręgu o środku 
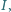stycznym do boków 
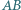i 
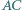w punktach 
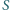i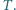 
Na boku 
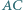leży taki punkt 
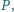że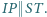 
Proste 
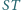i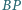 
przecinają się w punkcie 
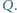Dowieść, że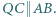 
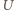punkt styczności boku 
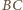z okręgiem wpisanym (rys.) i niech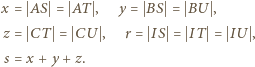
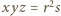(znany fakt - lub nietrudne ćwiczenie).
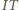jest wysokością w trójkącie prostokątnym 
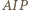; zatem 
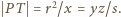Stąd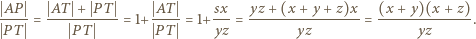
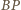przecina boki trójkąta 
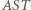(lub ich przedłużenia) w punktach 
więc w myśl wzoru Menelausa
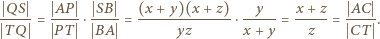
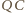i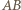 
(odwrócenie twierdzenie Talesa).