Klub 44M - zadania III 2017»Zadanie 737
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2017
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (67 KB)
Pięciokąt 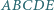 jest wpisany w okrąg
jest wpisany w okrąg 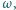 przy czym proste
przy czym proste 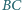 i
i 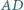 przecinają się w takim punkcie
przecinają się w takim punkcie 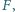 że prosta
że prosta 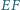 jest styczna do
jest styczna do 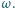 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 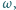 równoległa do
równoległa do 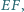 przecina proste
przecina proste 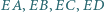 odpowiednio w punktach
odpowiednio w punktach 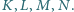 Udowodnić, że odcinki
Udowodnić, że odcinki 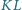 i
i 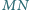 mają jednakową długość.
mają jednakową długość.


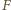 prostą różną od
prostą różną od 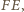 styczną do okręgu
styczną do okręgu 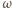 w punkcie
w punkcie 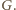 Prosta przechodząca przez punkty
Prosta przechodząca przez punkty 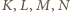 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 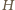 i przecina prostą
i przecina prostą 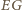 w punkcie
w punkcie 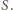 Pokażemy, że
Pokażemy, że 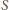 jest środkiem odcinka
jest środkiem odcinka 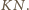 Ponieważ
Ponieważ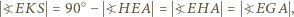
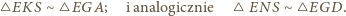
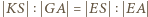 oraz
oraz 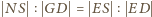 ; a z nich -
; a z nich -
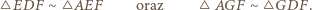
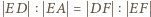 oraz
oraz 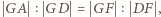 z których wynika, że prawa strona wzoru (1) jest równa
z których wynika, że prawa strona wzoru (1) jest równa 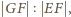 czyli 1.
czyli 1.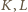 leżą po jednej stronie punktu
leżą po jednej stronie punktu 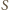 ; punkty
; punkty 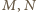 po drugiej. Uzyskana równość
po drugiej. Uzyskana równość 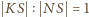 oznacza, że
oznacza, że 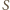 jest środkiem odcinka
jest środkiem odcinka 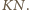 Przez analogię, ten sam punkt
Przez analogię, ten sam punkt 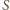 jest też środkiem odcinka
jest też środkiem odcinka 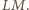 Stąd wniosek, że odcinki
Stąd wniosek, że odcinki 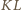 i
i 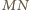 są przystające.
są przystające.