Dwa trójkąty»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Dwa trójkąty
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (97 KB)
Twierdzenie (Pascala). Punkty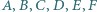 
leżą na jednym okręgu. Proste 
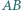i 
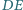przecinają się w punkcie 
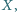proste 
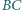i 
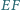w punkcie 
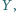proste 
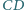i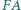 
w punkcie 
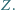Wykaż, że wówczas punkty 
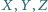leżą na jednej prostej.
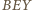przecina proste 
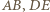w drugich punktach odpowiednio 
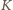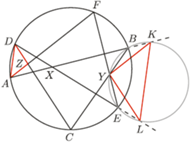
i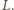 
Dowód przeprowadzimy w przypadku przedstawionym na rysunku, pozostałe można uzasadnić podobnie.
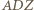i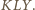 
Z równości kątów wpisanych opartych na jednym łuku mamy 
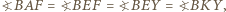więc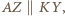 
ponieważ punkty 
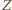i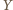 
leżą po przeciwnych stronach prostej 
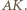Podobnie 
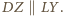Ponadto czworokąt 
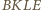jest wpisany w okrąg, zatem 
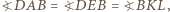a stąd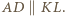 
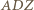i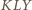 
spełniają założenia twierdzenia 
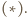Stąd punkt 
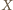przecięcia prostych 
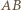i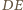 
należy też do prostej 