Dwa trójkąty»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Dwa trójkąty
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (97 KB)
Dany jest sześciokąt wypukły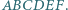 
Każda z przekątnych 
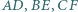dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
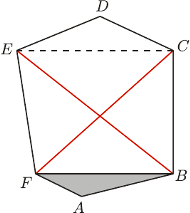
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/1x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif)
oznacza pole figury 
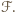Skoro ![1 |[BACF] = 2[BACDEF] = [ABEF],](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/3x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif)
to ![|[FBC] = [FBE].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/4x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif)
Trójkąty te mają wspólną podstawę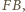 
zatem mają też równe wysokości na nią. Ponieważ punkty 
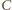i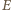 
leżą po tej samej stronie prostej 
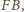wynika stąd, że 
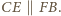Analogicznie 
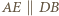oraz 
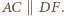
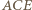i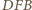 
spełniają założenia twierdzenia 
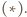Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków 