O własnościach prostej Simsona»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu O własnościach prostej Simsona
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (2417 KB)
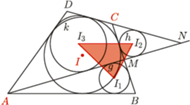
W czworokącie 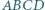 opisanym na okręgu prosta
opisanym na okręgu prosta 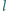 przechodząca przez wierzchołek
przechodząca przez wierzchołek 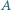 przecina bok
przecina bok 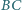 w punkcie
w punkcie 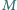 oraz półprostą
oraz półprostą 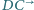 w punkcie
w punkcie 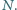 Punkty
Punkty 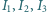 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 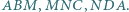 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 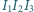 leży na prostej
leży na prostej 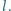

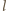 przecina półprostą
przecina półprostą 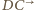 w punkcie
w punkcie 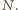 Trójki punktów
Trójki punktów 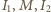 oraz
oraz 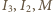 są, oczywiście, współliniowe. Oznaczmy przez
są, oczywiście, współliniowe. Oznaczmy przez 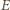 przecięcie prostych
przecięcie prostych 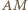 i drugiej stycznej poprowadzonej z punktu
i drugiej stycznej poprowadzonej z punktu 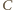 do okręgu o środku w punkcie
do okręgu o środku w punkcie 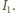 Łatwo zauważyć, że
Łatwo zauważyć, że 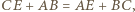 więc
więc 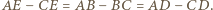 Oznacza to, że półprosta
Oznacza to, że półprosta 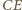 jest również styczna do okręgu o środku w punkcie
jest również styczna do okręgu o środku w punkcie 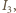 stąd punkty
stąd punkty 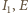 i
i 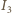 są współliniowe. Wobec tego
są współliniowe. Wobec tego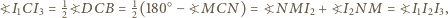
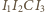 można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu
można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu 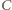 w symetrii względem prostych
w symetrii względem prostych 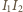 oraz
oraz 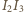 leżą na prostej
leżą na prostej  i zastosować twierdzenie Steinera.
i zastosować twierdzenie Steinera.