O własnościach prostej Simsona»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu O własnościach prostej Simsona
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (2417 KB)
Dany jest równoległobok 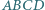 oraz punkt
oraz punkt 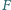 leżący na odcinku
leżący na odcinku 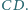 Punkty
Punkty 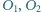 i
i 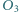 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 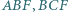 i
i 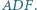 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 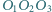 leży na prostej
leży na prostej 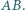

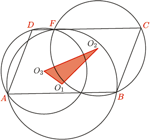
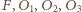 leżą na jednym okręgu. Istotnie,
leżą na jednym okręgu. Istotnie,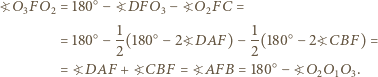
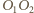 i
i 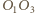 są prostopadłe odpowiednio do
są prostopadłe odpowiednio do 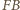 i
i 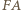 ). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu
). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu 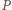 względem boków trójkąta
względem boków trójkąta 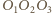 leżą na prostej
leżą na prostej 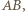 jednakże jest to oczywiste, gdyż proste
jednakże jest to oczywiste, gdyż proste 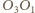 oraz
oraz 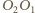 są symetralnymi odcinków odpowiednio
są symetralnymi odcinków odpowiednio 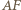 i
i