Klub 44M - zadania I 2017»Zadanie 725
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2017
- Publikacja w Delcie: styczeń 2017
- Publikacja elektroniczna: 30 grudnia 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (74 KB)
W czworokącie wypukłym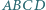 
kąty przy wierzchołkach 
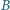i 
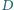są proste. Przekątne przecinają się w punkcie 
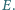Prosta prostopadła do 
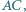przechodząca przez punkt 
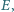przecina proste 
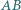i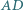 
w punktach 
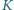i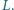 
Wykazać, że punkty 
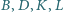leżą na jednym okręgu.
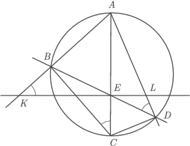
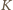i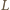 
pokrywają się z 
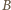i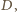 
i nie ma czego dowodzić. Przyjmijmy dalej, nie tracąc ogólności, że kąt 
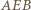jest ostry (wtedy punkt 
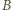leży między 
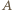i 
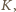zaś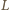 
leży między 
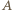i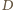 
). Czworokąt 
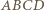ma okrąg opisany (o średnicy 
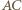). Stąd oraz z zależności w trójkątach prostokątnych 
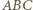i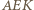 
dostajemy ciąg równości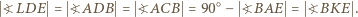
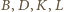na wspólnym okręgu.