Klub 44M - zadania V 2016»Zadanie 721
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2016
- Publikacja w Delcie: maj 2016
- Publikacja elektroniczna: 1 maja 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (106 KB)
Na bokach 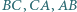 trójkąta
trójkąta 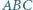 leżą punkty
leżą punkty 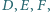 w których okręgi dopisane do trójkąta są styczne do tych boków. Niech
w których okręgi dopisane do trójkąta są styczne do tych boków. Niech 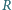 i
i  będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów
będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów 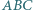 i
i 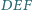 wynosi
wynosi 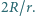

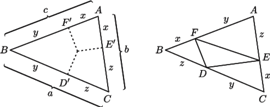
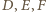 są położone na bokach
są położone na bokach 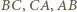 symetrycznie (względem środków owych boków) do punktów
symetrycznie (względem środków owych boków) do punktów 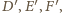 w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia:
w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia: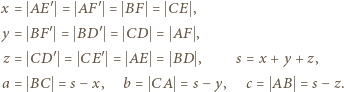
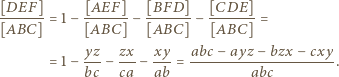
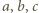 przez
przez 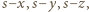 otrzymujemy po krótkim rachunku wzór
otrzymujemy po krótkim rachunku wzór![EF] [D----- 2xyz- [ABC]= abc .](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/4x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
 i
i 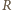 to promienie okręgów wpisanego i opisanego):
to promienie okręgów wpisanego i opisanego):![[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/7x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
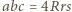 oraz
oraz 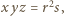 które po wprowadzeniu do równości
które po wprowadzeniu do równości 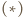 dają tezę zadania.
dają tezę zadania.