Dwusieczne»Zadanie 3
o zadaniu...
- Zadanie olimpijskie: LXVI Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Dwusieczne
- Publikacja w Delcie: kwiecień 2016
- Publikacja elektroniczna: 30 marca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Dany jest trójkąt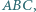 
w którym kąt przy wierzchołku 
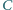jest prosty. Punkt 
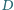jest spodkiem wysokości opuszczonej z wierzchołka 
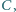a okrąg wpisany w dany trójkąt jest styczny do boków 
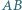i 
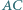odpowiednio w punktach 
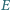i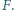 
Wykaż, że ortocentrum trójkąta 
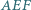jest środkiem okręgu wpisanego w trójkąt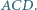 
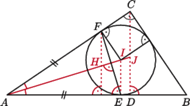
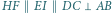
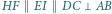
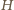ortocentrum trójkąta 
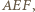przez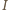 
środek okręgu wpisanego w trójkąt 
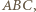a przez 
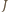punkt przecięcia prostych 
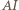i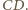 
Ponieważ 
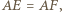więc półprosta 
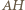jest dwusieczną kąta 
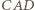i do zakończenia dowodu wystarczy wykazać, że półprosta 
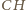jest dwusieczną kąta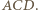 
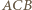jest prosty, więc punkty 
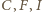i punkt styczności okręgu wpisanego w trójkąt 
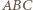z bokiem 
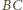tworzą kwadrat. Stąd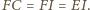 
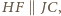równości odcinków, twierdzenia Talesa dla 
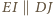i twierdzenia o dwusiecznej, uzyskujemy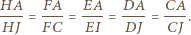
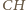jest dwusieczną kąta 