Dwusieczne»Zadanie 1
o zadaniu...
- Zadanie olimpijskie: LXIV Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Dwusieczne
- Publikacja w Delcie: kwiecień 2016
- Publikacja elektroniczna: 30 marca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Dany jest czworokąt wypukły 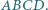 Proste zawierające dwusieczne kątów wewnętrznych
Proste zawierające dwusieczne kątów wewnętrznych 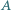 i
i 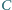 przecinają się w punkcie
przecinają się w punkcie 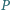 leżącym wewnątrz czworokąta
leżącym wewnątrz czworokąta 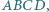 a proste zawierające dwusieczne kątów wewnętrznych
a proste zawierające dwusieczne kątów wewnętrznych 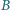 i
i 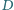 przecinają się w punkcie
przecinają się w punkcie 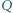 na zewnątrz czworokąta. Udowodnij, że jeżeli kąt
na zewnątrz czworokąta. Udowodnij, że jeżeli kąt 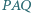 jest prosty, to również kąt
jest prosty, to również kąt 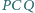 jest prosty.
jest prosty.

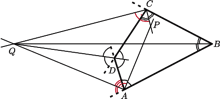
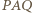 jest prosty, to
jest prosty, to 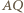 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 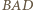 czworokąta. Z kolei aby dowieść, że kąt
czworokąta. Z kolei aby dowieść, że kąt 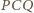 jest prosty, wystarczy wykazać, że
jest prosty, wystarczy wykazać, że 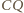 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 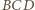 czworokąta.
czworokąta.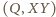 odległość punktu
odległość punktu 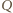 od prostej
od prostej 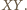 Zachodzą równości
Zachodzą równości 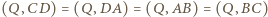 oraz
oraz 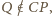 co kończy dowód.
co kończy dowód.