Klub 44M - zadania III 2016»Zadanie 717
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2016
- Publikacja w Delcie: marzec 2016
- Publikacja elektroniczna: 29 lutego 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Dany jest trójkąt 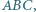 w którym
w którym 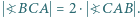 Odcinek
Odcinek 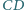 (o końcu
(o końcu 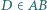 ) jest dwusieczną kąta
) jest dwusieczną kąta 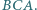 Punkt
Punkt 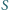 jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach
jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach 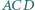 i
i 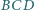 oraz stycznego do półprostej
oraz stycznego do półprostej 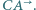 Udowodnić, że proste
Udowodnić, że proste 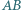 i
i 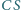 są prostopadłe.
są prostopadłe.

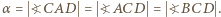 Duży okrąg o środku
Duży okrąg o środku 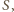 którego dotyczy zadanie, oznaczmy symbolem
którego dotyczy zadanie, oznaczmy symbolem 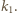 Okręgi opisane na trójkątach
Okręgi opisane na trójkątach 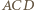 i
i 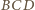 oznaczmy przez
oznaczmy przez 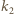 i
i 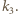 Niech
Niech 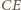 będzie cięciwą okręgu
będzie cięciwą okręgu 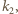 równoległą do
równoległą do 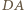 (zatem
(zatem 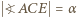 ), i niech
), i niech 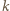 będzie okręgiem o środku
będzie okręgiem o środku 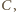 stycznym do prostej
stycznym do prostej 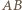 w punkcie
w punkcie 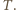 Skoro
Skoro 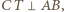 teza zadania sprowadza się do wykazania, że punkt
teza zadania sprowadza się do wykazania, że punkt 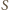 leży na prostej
leży na prostej 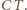
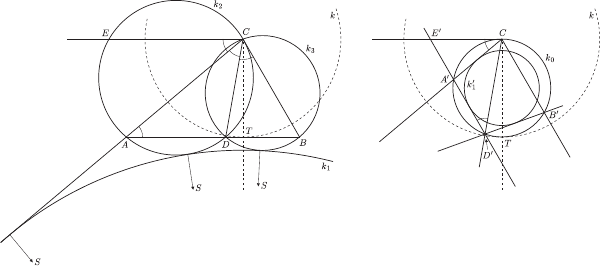
 Każda z półprostych
Każda z półprostych 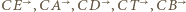 (bez punktu
(bez punktu 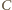 ) jest odwzorowywana na samą siebie. Prosta
) jest odwzorowywana na samą siebie. Prosta 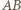 przechodzi na okrąg
przechodzi na okrąg 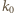 o średnicy
o średnicy 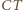 (punkt
(punkt 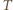 nie zmienia położenia). Obrazami punktów
nie zmienia położenia). Obrazami punktów 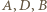 są punkty
są punkty 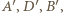 w których półproste
w których półproste 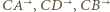 przecinają okrąg
przecinają okrąg 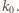 Okręgi
Okręgi 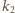 i
i 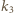 (bez punktu
(bez punktu 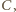 który jest środkiem inwersji) zostają przekształcone na proste
który jest środkiem inwersji) zostają przekształcone na proste 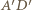 oraz
oraz 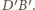 Obrazem okręgu
Obrazem okręgu 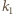 jest okrąg
jest okrąg 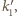 styczny do prostych
styczny do prostych 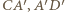 i
i 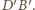
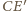 jest styczna do okręgu
jest styczna do okręgu 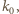 więc
więc 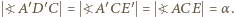
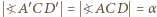 oraz
oraz 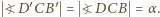 Zatem cięciwy
Zatem cięciwy 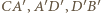 okręgu
okręgu 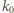 są jednakowej długości. Okrąg
są jednakowej długości. Okrąg 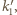 styczny do tych trzech cięciw, jest wobec tego współśrodkowy z okręgiem
styczny do tych trzech cięciw, jest wobec tego współśrodkowy z okręgiem 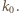 Prosta
Prosta 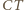 jest więc osią symetrii okręgu
jest więc osią symetrii okręgu 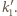
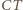 jest też osią symetrii okręgu
jest też osią symetrii okręgu 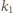 - przechodzi zatem przez jego środek, czyli punkt
- przechodzi zatem przez jego środek, czyli punkt 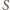 - a to właśnie mieliśmy wykazać.
- a to właśnie mieliśmy wykazać.