Klub 44M - zadania I 2016»Zadanie 713
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2016
- Publikacja w Delcie: styczeń 2016
- Publikacja elektroniczna: 1 stycznia 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
Dany jest czworokąt wypukły 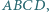 w którym boki
w którym boki 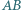 i
i 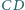 nie są równoległe. Rozważamy okrąg, przechodzący przez punkty
nie są równoległe. Rozważamy okrąg, przechodzący przez punkty 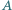 i
i 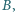 styczny do prostej
styczny do prostej 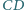 w punkcie
w punkcie 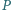 oraz okrąg, przechodzący przez punkty
oraz okrąg, przechodzący przez punkty 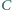 i
i 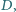 styczny do prostej
styczny do prostej 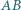 w punkcie
w punkcie 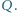 Zakładamy, że punkty
Zakładamy, że punkty 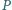 i
i 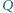 leżą na odcinkach
leżą na odcinkach 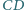 i
i 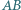 oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka
oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka 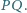 Udowodnić, że proste
Udowodnić, że proste 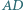 i
i 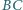 są równoległe.
są równoległe.

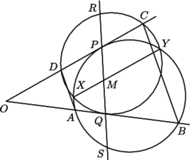
 przecięcia prostych
przecięcia prostych 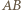 i
i 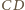 leży na półprostych
leży na półprostych 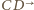 i
i 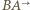 oraz że prosta
oraz że prosta 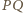 przecina okręgi
przecina okręgi 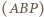 i
i 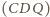 odpowiednio w punktach
odpowiednio w punktach 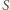 i
i 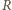 (różnych od
(różnych od 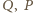 ). Wspólna cięciwa tych okręgów - nazwijmy ją
). Wspólna cięciwa tych okręgów - nazwijmy ją 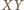 - przechodzi przez środek
- przechodzi przez środek 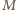 odcinka
odcinka 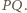 Z równości
Z równości 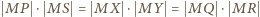 oraz
oraz 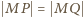 wnosimy, że
wnosimy, że 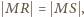 a stąd
a stąd 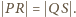
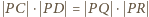 oraz
oraz 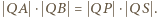 Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów
Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów 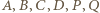 od punktu
od punktu 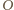 kolejno literami
kolejno literami 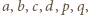 przepisujemy uzyskaną zależność w postaci
przepisujemy uzyskaną zależność w postaci 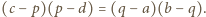 Po wymnożeniu i uwzględnieniu równości
Po wymnożeniu i uwzględnieniu równości 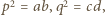 otrzymujemy związek
otrzymujemy związek 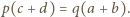 Tak więc
Tak więc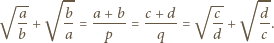
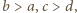 wynika stąd, że
wynika stąd, że 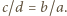 To zaś oznacza, że proste
To zaś oznacza, że proste 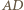 i
i 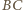 są równoległe.
są równoległe.