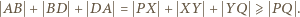Klub 44M - zadania VI 2015»Zadanie 703
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2015
- Publikacja w Delcie: czerwiec 2015
- Publikacja elektroniczna: 31 maja 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)
Dany jest czworokąt wypukły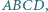 
w którym kąty wewnętrzne przy wierzchołkach 
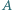oraz 
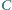są równe, przy tym ostre. Punkty 
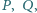leżące odpowiednio na półprostych 
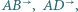są wyznaczone przez warunki 
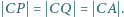Wykazać, że długość odcinka 
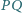nie przekracza obwodu trójkąta 
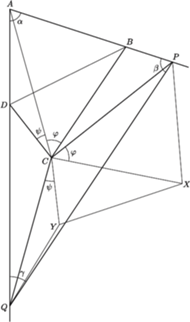
leży wewnątrz trójkąta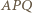 
(jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego 
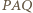). Oznaczmy kąty tego trójkąta: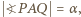 
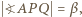
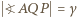; ponadto niech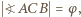 
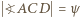; z założenia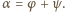 
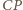i 
czworokąta (wklęsłego)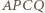 
budujemy, po zewnętrznej jego stronie, trójkąty 
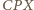i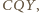 
przystające odpowiednio do trójkątów 
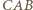i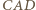 
:
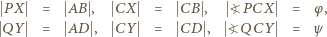
leży między 
i 
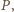zaś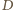 
między 
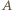i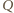 
; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro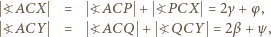
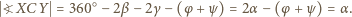
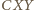jest przystający do trójkąta 
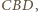wobec czego 
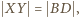i otrzymujemy tezę zadania: