Niech 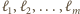 będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że
będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że 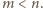 Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych
Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych 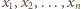 w taki sposób, aby suma na każdej prostej
w taki sposób, aby suma na każdej prostej 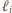 była równa
była równa 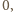 ale aby nie wszystkie liczby
ale aby nie wszystkie liczby 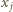 były równe
były równe 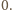 Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych
Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych

o  równaniach i
równaniach i 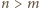 niewiadomych ma nietrywialne rozwiązanie.
niewiadomych ma nietrywialne rozwiązanie.
W szczególności prawdziwa jest zależność
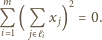
Po wymnożeniu i uporządkowaniu składników widzimy, że lewa strona powyższej równości składa się z wyrazów postaci 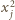 oraz
oraz 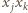 dla
dla 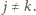 Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci
Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci 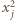 występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby
występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby 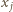 i
i 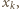 gdzie
gdzie 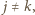 znajdą się razem w dokładnie jednej sumie. A zatem przy składniku
znajdą się razem w dokładnie jednej sumie. A zatem przy składniku 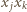 znajduje się współczynnik
znajduje się współczynnik 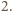 W tej sytuacji
W tej sytuacji
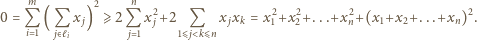
Stąd jednak wynika, że 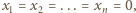 co stanowi sprzeczność z wyborem liczb
co stanowi sprzeczność z wyborem liczb 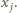 Kończy to dowód.
Kończy to dowód.
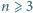 różnych punktów, które nie leżą wszystkie na jednej prostej. Udowodnić, że istnieje co najmniej
różnych punktów, które nie leżą wszystkie na jednej prostej. Udowodnić, że istnieje co najmniej 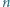 różnych prostych, z których każda zawiera co najmniej dwa spośród danych punktów.
różnych prostych, z których każda zawiera co najmniej dwa spośród danych punktów.
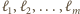 będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że
będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że 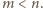 Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych
Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych 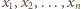 w taki sposób, aby suma na każdej prostej
w taki sposób, aby suma na każdej prostej 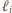 była równa
była równa 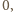 ale aby nie wszystkie liczby
ale aby nie wszystkie liczby 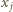 były równe
były równe 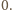 Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych
Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych
 równaniach i
równaniach i 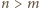 niewiadomych ma nietrywialne rozwiązanie.
niewiadomych ma nietrywialne rozwiązanie.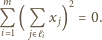
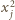 oraz
oraz 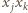 dla
dla 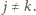 Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci
Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci 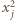 występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby
występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby 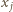 i
i 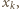 gdzie
gdzie 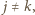 znajdą się razem w dokładnie jednej sumie. A zatem przy składniku
znajdą się razem w dokładnie jednej sumie. A zatem przy składniku 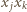 znajduje się współczynnik
znajduje się współczynnik  W tej sytuacji
W tej sytuacji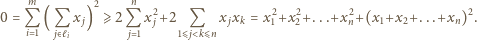
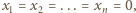 co stanowi sprzeczność z wyborem liczb
co stanowi sprzeczność z wyborem liczb  Kończy to dowód.
Kończy to dowód.