Klub 44M - zadania VI 2014»Zadanie 683
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2014
- Publikacja w Delcie: czerwiec 2014
- Publikacja elektroniczna: 2 czerwca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (89 KB)
Dane są dwa przystające okręgi, przecinające się w punktach 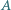 i
i 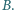 Punkt
Punkt 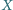 leży na jednym z tych okręgów, punkt
leży na jednym z tych okręgów, punkt 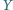 na drugim, przy czym prosta
na drugim, przy czym prosta 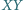 nie przechodzi ani przez
nie przechodzi ani przez 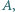 ani przez
ani przez 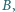 ani przez środek odcinka
ani przez środek odcinka 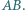 Punkt
Punkt 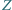 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 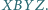 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 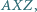
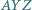 są przystające do dwóch danych okręgów.
są przystające do dwóch danych okręgów.


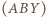 przez
przez 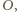 środek okręgu
środek okręgu 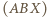 przez
przez 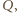 i niech
i niech 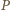 będzie punktem symetrycznym do
będzie punktem symetrycznym do 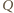 względem prostej
względem prostej 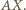 Czworokąty
Czworokąty 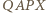 i
i 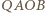 są rombami. Zatem
są rombami. Zatem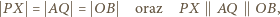
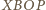 jest równoległobokiem. Również czworokąt
jest równoległobokiem. Również czworokąt 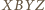 jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt
jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt 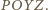 Wobec tego
Wobec tego 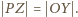
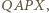 pokazuje, że odległość punktu
pokazuje, że odległość punktu 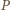 od każdego z trójki punktów
od każdego z trójki punktów 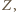
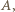
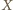 jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc,
jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc, 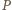 jest środkiem okręgu przystającego do nich i przechodzącego przez punkty
jest środkiem okręgu przystającego do nich i przechodzącego przez punkty 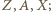 to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie
to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie 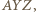 wynika z pierwszej przez symetrię (logiczną).
wynika z pierwszej przez symetrię (logiczną).