Klub 44M - zadania IV 2014»Zadanie 680
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2014
- Publikacja w Delcie: kwiecień 2014
- Publikacja elektroniczna: 31 marca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (580 KB)
Dwusieczne kątów wewnętrznych trójkąta
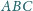 przecinają okrąg na nim
opisany odpowiednio w punktach
przecinają okrąg na nim
opisany odpowiednio w punktach
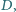
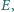
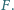 Odcinki prostych
Odcinki prostych
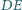 i
i
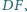 wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
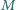 i
i
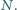 Odcinki
Odcinki
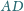 i
i
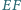 przecinają się w punkcie
przecinają się w punkcie
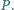 Wykazać, że
środek okręgu, przechodzącego przez punkty
Wykazać, że
środek okręgu, przechodzącego przez punkty
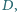
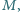
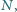 leży
na okręgu, przechodzącym przez punkty
leży
na okręgu, przechodzącym przez punkty
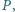
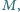
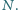

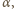
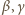 miary kątów trójkąta
miary kątów trójkąta
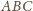 przy
wierzchołkach
przy
wierzchołkach
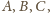 zaś przez
zaś przez
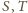 punkty przecięcia
odcinka
punkty przecięcia
odcinka
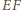 odpowiednio z bokami
odpowiednio z bokami
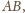
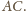 Odcinki
Odcinki
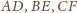 przecinają się w punkcie
przecinają się w punkcie
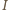 (środku okręgu
wpisanego). Z równości
(środku okręgu
wpisanego). Z równości
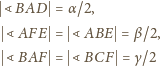
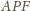 kąty przy wierzchołkach
kąty przy wierzchołkach
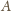 i
i
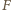 sumują się do kąta prostego. Zatem kąt przy
wierzchołku
sumują się do kąta prostego. Zatem kąt przy
wierzchołku
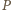 jest prosty. W trójkącie
jest prosty. W trójkącie
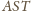 odcinek
odcinek
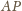 jest więc jednocześnie dwusieczną i wysokością; to znaczy, że
punkt
jest więc jednocześnie dwusieczną i wysokością; to znaczy, że
punkt
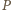 jest środkiem odcinka
jest środkiem odcinka
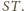
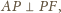 równość
równość
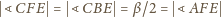
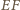 jest symetralną odcinka
jest symetralną odcinka
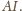 Przez analogię,
punkty
Przez analogię,
punkty
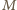 i
i
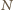 są środkami odcinków
są środkami odcinków
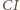 i
i
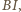 a proste
a proste
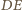 i
i
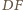 są symetralnymi tych odcinków. W takim razie
jednokładność o środku
są symetralnymi tych odcinków. W takim razie
jednokładność o środku
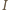 i skali
i skali
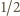 przekształca trójkąt
przekształca trójkąt
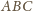 na trójkąt
na trójkąt
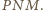
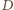 jest środek
jest środek
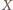 odcinka
odcinka
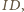 który
wobec tego leży na okręgu
który
wobec tego leży na okręgu
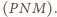 Pozostaje zauważyć, że
punkt
Pozostaje zauważyć, że
punkt
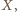 jako środek przeciwprostokątnej trójkątów prostokątnych
jako środek przeciwprostokątnej trójkątów prostokątnych
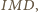
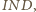 jest też środkiem okręgu
jest też środkiem okręgu