Klub 44M - zadania II 2014»Zadanie 676
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2014
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31 stycznia 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (237 KB)
Zadanie 676 zaproponował pan Tomasz Ordowski
W trójkącie o bokach długości
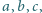 o wszystkich kątach
wewnętrznych mniejszych od
o wszystkich kątach
wewnętrznych mniejszych od
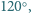 znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
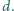 Dowieść,
że zachodzi równość
Dowieść,
że zachodzi równość


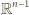 umieścimy sympleks foremny
o krawędzi
umieścimy sympleks foremny
o krawędzi
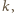 to dla dowolnego punktu tej przestrzeni, leżącego
w odległościach
to dla dowolnego punktu tej przestrzeni, leżącego
w odległościach
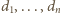 od jego wierzchołków, zachodzi
równość
od jego wierzchołków, zachodzi
równość
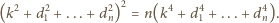
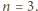
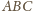 będzie trójkątem rozważanym obecnie, o bokach
będzie trójkątem rozważanym obecnie, o bokach
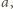
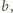
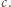 Punkt, o którym mowa, to punkt Toricellego (lub punkt
Fermata)
Punkt, o którym mowa, to punkt Toricellego (lub punkt
Fermata)
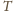 ; założenie o kątach
; założenie o kątach
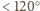 gwarantuje, że
gwarantuje, że
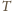 leży wewnątrz trójkąta, na przecięciu odcinków
leży wewnątrz trójkąta, na przecięciu odcinków
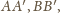
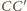 – gdzie litery z primami oznaczają wierzchołki trójkątów
równobocznych
– gdzie litery z primami oznaczają wierzchołki trójkątów
równobocznych
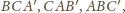 zbudowanych na zewnątrz trójkąta
zbudowanych na zewnątrz trójkąta
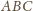 – to własność dobrze znana (wyprowadzenie i komentarze można
znaleźć w wielu miejscach; choćby http://pl.wikipedia.org/wiki/Punkt_Fermata).
– to własność dobrze znana (wyprowadzenie i komentarze można
znaleźć w wielu miejscach; choćby http://pl.wikipedia.org/wiki/Punkt_Fermata).
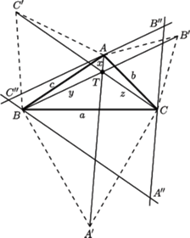
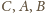 prowadzimy proste równoległe odpowiednio do
prowadzimy proste równoległe odpowiednio do
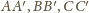 ; przecinając się, tworzą one trójkąt równoboczny
; przecinając się, tworzą one trójkąt równoboczny
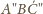 (oznaczenia jak na rysunku). W trapezach równoramiennych
(o kątach
(oznaczenia jak na rysunku). W trapezach równoramiennych
(o kątach
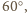
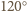 )
)
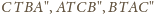 zachodzą
równości
zachodzą
równości
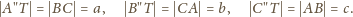
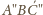 ma bok długości
ma bok długości
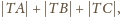 czyli
czyli
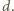
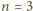 ) do trójkąta
) do trójkąta
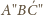 oraz punktu
oraz punktu
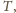 leżącego w odległościach
leżącego w odległościach
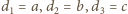 od
od
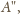
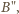
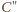 ; teraz
; teraz
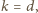 i mamy tezę zadania.
i mamy tezę zadania.