Klub 44M - zadania IX 2013»Zadanie 665
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2013
- Publikacja w Delcie: wrzesień 2013
- Publikacja elektroniczna: 31 sierpnia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (98 KB)
Dany jest równoległobok
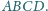 Punkty
Punkty
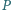 i
i
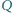 leżą
odpowiednio na bokach
leżą
odpowiednio na bokach
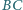 i
i
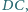 odcinki
odcinki
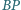 i
i
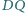 mają
jednakową długość. Dowieść, że odcinki
mają
jednakową długość. Dowieść, że odcinki
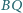 i
i
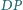 przecinają
się w punkcie, leżącym na dwusiecznej kąta
przecinają
się w punkcie, leżącym na dwusiecznej kąta
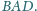


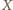 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków
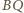 i
i
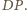 Przedłużamy
odcinek
Przedłużamy
odcinek
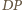 do przecięcia z prostą
do przecięcia z prostą
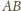 w punkcie
w punkcie
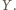 Z równoległości
Z równoległości
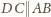 oraz
oraz
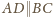 wynikają
proporcje
wynikają
proporcje

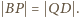 Zatem i lewe strony mają jednakową wartość; a to znaczy,
że w trójkącie
Zatem i lewe strony mają jednakową wartość; a to znaczy,
że w trójkącie
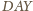 odcinek
odcinek
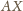 jest dwusieczną kąta przy
wierzchołku
jest dwusieczną kąta przy
wierzchołku
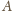 (czy go nazwiemy
(czy go nazwiemy
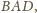 czy
czy
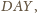 to
wszystko jedno).
to
wszystko jedno).