W krzywym zwierciadle»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: XLVIII Olimpiada Matematyczna
- Zadanie pochodzi z artykułu W krzywym zwierciadle
- Publikacja w Delcie: maj 2013
- Publikacja elektroniczna: 30-04-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (68 KB)
Okrąg o środku w punkcie
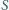 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
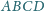 jest styczny do boków
jest styczny do boków
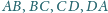 odpowiednio
w punktach
odpowiednio
w punktach
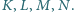 Proste
Proste
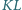 i
i
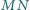 przecinają
się w punkcie
przecinają
się w punkcie
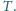 Wykaż, że proste
Wykaż, że proste
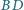 i
i
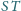 są
prostopadłe.
są
prostopadłe.


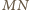 w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
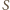 i przez stałe
punkty
i przez stałe
punkty
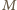 i
i
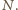 Leży na nim też punkt
Leży na nim też punkt
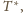 bo
punkt
bo
punkt
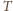 leży na prostej
leży na prostej
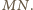 Średnicą tego okręgu jest
Średnicą tego okręgu jest
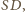 ponieważ kąty
ponieważ kąty
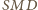 i
i
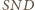 są proste, stąd także
są proste, stąd także
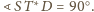
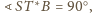 więc
więc
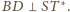 Z definicji inwersji
punkty
Z definicji inwersji
punkty
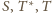 są współliniowe, co kończy dowód.
są współliniowe, co kończy dowód.