Klub 44M - zadania II 2013»Zadanie 655
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2013
- Publikacja w Delcie: luty 2013
- Publikacja elektroniczna: 31 stycznia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (192 KB)
Punkt
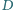 leży na boku
leży na boku
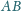 trójkąta
trójkąta
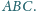 Punkt
Punkt
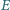 jest środkiem okręgu dopisanego, stycznego do boku
jest środkiem okręgu dopisanego, stycznego do boku
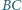 oraz
przedłużeń boków
oraz
przedłużeń boków
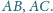 Punkt
Punkt
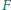 jest środkiem
okręgu wpisanego w trójkąt
jest środkiem
okręgu wpisanego w trójkąt
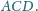 Dowieść, że jeżeli trójkąt
Dowieść, że jeżeli trójkąt
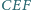 jest równoramienny, to także trójkąt
jest równoramienny, to także trójkąt
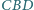 jest
równoramienny.
jest
równoramienny.

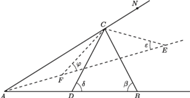
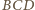 przy wierzchołkach
przy wierzchołkach
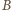 i
i
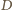 przez
przez
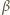 i
i
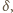 a miary kątów trójkąta
a miary kątów trójkąta
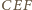 przy
wierzchołkach
przy
wierzchołkach
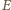 i
i
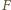 przez
przez
 i
i
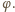
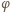 i
i
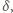 jako kąty zewnętrzne trójkątów
jako kąty zewnętrzne trójkątów
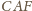 i
i
 są związane zależnością
są związane zależnością
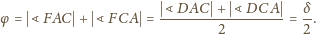
 będzie dowolnym punktem na przedłużeniu boku
będzie dowolnym punktem na przedłużeniu boku
 poza wierzchołek
poza wierzchołek
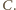 Kąty
Kąty
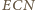 i
i
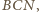 jako
kąty zewnętrzne trójkątów
jako
kąty zewnętrzne trójkątów
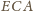 i
i
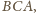 wyrażają się
jako sumy:
wyrażają się
jako sumy:
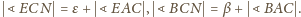 Tak
więc
Tak
więc
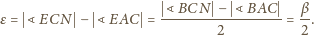
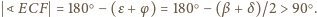 Zatem jeśli
trójkąt
Zatem jeśli
trójkąt
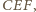 z kątem rozwartym przy wierzchołku
z kątem rozwartym przy wierzchołku
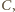 jest
równoramienny, to
jest
równoramienny, to
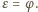 Z uzyskanych wcześniej równości
dostajemy wówczas
Z uzyskanych wcześniej równości
dostajemy wówczas
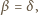 czyli równoramienność trójkąta
czyli równoramienność trójkąta