Klub 44M - zadania IX 2012»Zadanie 645
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2012
- Publikacja w Delcie: wrzesień 2012
- Publikacja elektroniczna: 3 września 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (91 KB)
Czworokąt
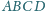jest wpisany w okrąg. Boki
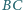i
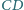mają
jednakową długość. Na przedłużeniu odcinka
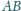odkładamy odcinek
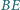długości
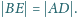Dowieść, że
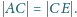
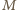i
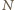będą rzutami prostokątnymi punktu
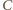odpowiednio na proste
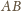i
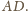Punkt
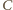(środek łuku
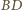) leży na dwusiecznej kąta
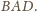Zatem
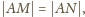
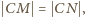trójkąty
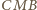i
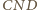są przystające,
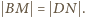Są możliwe dwie konfiguracje: albo (jak na rysunku) punkt
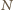leży między punktami
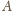i
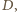a
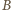między
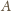i
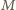– albo odwrotnie (
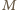między
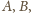zaś
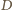między
).
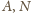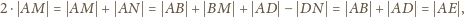
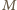jest środkiem odcinka
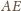(rozumowanie
w drugim przypadku, po oczywistej zmianie w znakach, prowadzi do tej
samej konkluzji). Wniosek: prosta
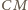jest symetralną odcinka
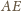i wobec tego
