- Narzędzia
- Obiekty
- Słowa kluczowe
- Kategoria
- Planimetria
O LXIII Olimpiadzie Matematycznej»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu O LXIII Olimpiadzie Matematycznej
- Publikacja w Delcie: lipiec 2012
- Publikacja elektroniczna: 01-07-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (69 KB)
W trójkącie ostrokątnym
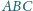 punkt
punkt
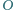 jest środkiem okręgu
opisanego, a dwusieczna kąta
jest środkiem okręgu
opisanego, a dwusieczna kąta
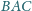 przecina bok
przecina bok
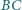 w punkcie
w punkcie
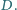 Niech
Niech
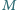 będzie takim punktem, że
będzie takim punktem, że
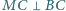 oraz
oraz
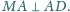 Proste
Proste
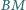 i
i
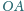 przecinają się w punkcie
przecinają się w punkcie
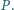 Wykazać, że okrąg o środku
Wykazać, że okrąg o środku
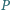 i przechodzący przez punkt
i przechodzący przez punkt
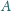 jest styczny do prostej
jest styczny do prostej
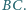
Rozwiązanie
Przedstawione rozwiązanie jest prawie analityczne, oparte na idei, która
zapewne powstała po przyjrzeniu się dokładnemu rysunkowi, który
był w brudnopisie (zamieszczamy go na dole sąsiedniej szpalty). Niech
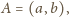
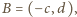
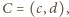
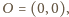
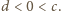 Ponieważ
trójkąt
Ponieważ
trójkąt
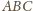 jest ostrokątny, więc
jest ostrokątny, więc
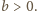 Możemy założyć, że
promień okręgu opisanego na trójkącie
Możemy założyć, że
promień okręgu opisanego na trójkącie
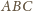 jest równy
jest równy
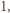 więc
więc
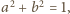
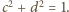 Ponieważ
Ponieważ
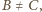 więc
więc
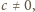 zatem
zatem
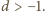 Niech
Niech
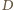 oznacza punkt wspólny boku
oznacza punkt wspólny boku
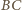 i dwusiecznej kąta
i dwusiecznej kąta
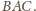 Jej równanie to
Jej równanie to
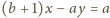 (bo
leżą na niej punkty
(bo
leżą na niej punkty
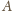 i
i
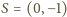 – środek łuku
– środek łuku
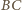 ). Wobec tego
). Wobec tego
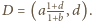 Równanie prostej
Równanie prostej
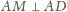 to
to
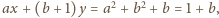 więc
więc
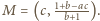 Niech
Niech
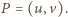 Mamy
Mamy
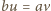 oraz
oraz
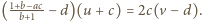 Jeśli
Jeśli
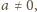 to
to
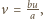 więc
więc
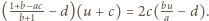 Stąd
Stąd

Stąd wynika, że prosta
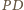 jest równoległa do prostej
jest równoległa do prostej
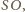 więc
trójkąty
więc
trójkąty
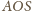 i
i
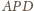 są podobne, zatem
są podobne, zatem
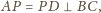 co
kończy dowód twierdzenia. Jeśli
co
kończy dowód twierdzenia. Jeśli
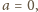 to
to
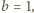 więc
więc
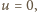 zatem
zatem
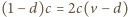 i
i
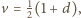 więc
więc
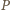 jest środkiem odcinka
jest środkiem odcinka
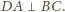 Twierdzenie zachodzi
również w tym przypadku.
Twierdzenie zachodzi
również w tym przypadku.
