Klub 44M - zadania V 2012»Zadanie 641
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2012
- Publikacja w Delcie: maj 2012
- Publikacja elektroniczna: 28 kwietnia 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)
Na płaszczyźnie dane są punkty
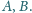 Rozważamy wszystkie
czworokąty wypukłe
Rozważamy wszystkie
czworokąty wypukłe
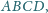 położone w ustalonej półpłaszczyźnie
o krawędzi
położone w ustalonej półpłaszczyźnie
o krawędzi
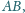 symetryczne względem prostej
symetryczne względem prostej
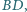 z kątem
prostym przy wierzchołku
z kątem
prostym przy wierzchołku
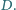 Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
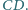

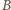 prowadzimy półprostą
prowadzimy półprostą
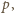 prostopadłą do
prostopadłą do
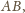 położoną w rozpatrywanej półpłaszczyźnie. Niech
położoną w rozpatrywanej półpłaszczyźnie. Niech
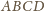 będzie jednym z rozważanych czworokątów. Trójkąt
będzie jednym z rozważanych czworokątów. Trójkąt
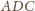 jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
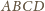 ) wynika, że punkt
) wynika, że punkt
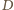 leży po tej stronie
leży po tej stronie
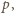 co
punkt
co
punkt
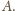 Półprosta
Półprosta
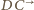 przecina więc
przecina więc
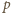 w pewnym
punkcie
w pewnym
punkcie
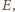 tworząc czworokąt wypukły
tworząc czworokąt wypukły
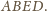 Ma on kąty proste
przy wierzchołkach
Ma on kąty proste
przy wierzchołkach
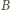 i
i
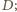 można na nim opisać okrąg.
Zatem
można na nim opisać okrąg.
Zatem
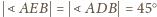 (ostatnia równość zachodzi,
bo
(ostatnia równość zachodzi,
bo
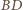 jest symetralną odcinka
jest symetralną odcinka
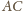 ). Stąd wniosek, że
). Stąd wniosek, że
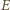 jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
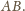 Jest to szukany punkt wspólny wszystkich możliwych prostych
Jest to szukany punkt wspólny wszystkich możliwych prostych