Klub 44M - zadania IV 2012»Zadanie 639
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2012
- Publikacja w Delcie: kwiecień 2012
- Publikacja elektroniczna: 1 kwietnia 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (78 KB)
W trójkącie
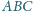 punkt
punkt
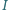 jest środkiem okręgu wpisanego.
Prosta
jest środkiem okręgu wpisanego.
Prosta
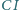 przecina bok
przecina bok
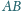 w punkcie
w punkcie
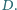 Prowadzimy
przez punkt
Prowadzimy
przez punkt
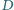 dowolną prostą, przecinającą okrąg opisany na
trójkącie
dowolną prostą, przecinającą okrąg opisany na
trójkącie
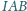 w punktach
w punktach
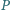 i
i
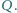 Wykazać, że prosta
Wykazać, że prosta
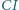 jest dwusieczną kąta
jest dwusieczną kąta
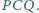


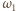 i
i
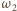 będą (odpowiednio) okręgami opisanymi
na trójkątach
będą (odpowiednio) okręgami opisanymi
na trójkątach
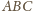 i
i
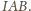 Dwusieczna
Dwusieczna
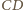 kąta
kąta
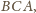 a raczej jej przedłużenie, przecina okrąg
a raczej jej przedłużenie, przecina okrąg
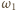 w środku
łuku
w środku
łuku
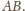 Oznaczmy ten punkt przez
Oznaczmy ten punkt przez
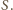 Zachodzi równość
Zachodzi równość
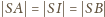 (znana, a przy tym łatwa do wykazania). Punkt
(znana, a przy tym łatwa do wykazania). Punkt
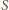 jest więc środkiem okręgu
jest więc środkiem okręgu
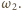 Zatem
Zatem
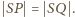
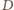 przecinają się cięciwy
przecinają się cięciwy
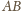 i
i
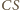 okręgu
okręgu
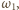 a także cięciwy
a także cięciwy
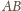 i
i
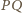 okręgu
okręgu
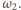 Tak
więc
Tak
więc
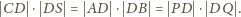
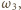 przechodzący przez punkty
przechodzący przez punkty
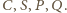 Jego cięciwy
Jego cięciwy
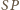 i
i
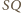 mają jednakową długość, więc wyznaczają przystające
łuki
mają jednakową długość, więc wyznaczają przystające
łuki
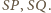 Oparte na nich kąty
Oparte na nich kąty
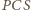 i
i
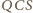 (wpisane
w okrąg
(wpisane
w okrąg
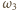 ) są równe – a to jest teza zadania.
) są równe – a to jest teza zadania.