Osie potęgowe»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Osie potęgowe
- Publikacja w Delcie: marzec 2012
- Publikacja elektroniczna: 02-03-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (90 KB)
Zadanie pochodzi z XLVI Olimpiady Matematycznej
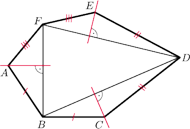
Sześciokąt
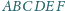 jest wypukły oraz
jest wypukły oraz
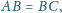
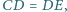
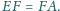 Wykaż, że proste zawierające
wysokości trójkątów
Wykaż, że proste zawierające
wysokości trójkątów
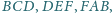 poprowadzone odpowiednio
z wierzchołków
poprowadzone odpowiednio
z wierzchołków
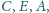 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.

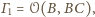
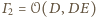 oraz
oraz
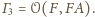 Punkt
Punkt
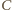 należy do
należy do
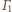 i
i
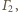 więc osią potęgową
tych okręgów jest rozważana w zadaniu prosta przechodząca przez
więc osią potęgową
tych okręgów jest rozważana w zadaniu prosta przechodząca przez
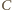 i prostopadła do prostej
i prostopadła do prostej
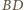 łączącej ich środki. Pozostałe
rozważane proste są osiami potęgowymi okręgów
łączącej ich środki. Pozostałe
rozważane proste są osiami potęgowymi okręgów
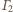 i
i
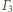 oraz
oraz
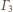 i
i
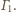 Środki
Środki
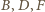 okręgów nie są współliniowe,
więc osie potęgowe przecinają się w jednym punkcie.
okręgów nie są współliniowe,
więc osie potęgowe przecinają się w jednym punkcie.