Izogonalnie sprzężone»Zadanie 1
o zadaniu...
- Zadanie olimpijskie: LI Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Izogonalnie sprzężone
- Publikacja w Delcie: listopad 2010
- Publikacja elektroniczna: 20-12-2010
- Artykuł źródłowy w wersji do druku [application/pdf]: (89 KB)
Dany jest trójkąt
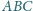 , w którym
, w którym
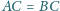 . Punkt
. Punkt
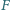 leży
wewnątrz trójkąta
leży
wewnątrz trójkąta
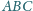 , przy czym
, przy czym
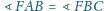 . Punkt
. Punkt
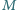 jest środkiem boku
jest środkiem boku
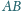 . Udowodnij, że
. Udowodnij, że
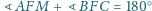 .
.

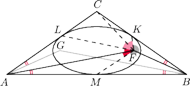
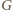 będzie obrazem
będzie obrazem
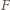 w symetrii względem prostej
w symetrii względem prostej
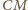 .
Wtedy
.
Wtedy
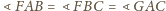 oraz
oraz
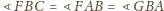 .
Z ćwiczenia (c) istnieje więc elipsa o ogniskach
.
Z ćwiczenia (c) istnieje więc elipsa o ogniskach
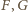 , wpisana w trójkąt
, wpisana w trójkąt
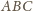 . Jest ona styczna do boku
. Jest ona styczna do boku
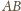 w punkcie
w punkcie
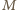 i do boków
i do boków
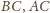 odpowiednio w
odpowiednio w
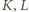 . Z Faktu,
. Z Faktu,
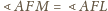 ,
,
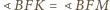 ,
,
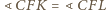 . Suma tych sześciu kątów daje
kąt pełny
. Suma tych sześciu kątów daje
kąt pełny
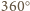 , zatem
, zatem
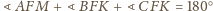 , co
kończy dowód.
, co
kończy dowód.