Klub 44M - zadania V 2013»Zadanie 662
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2013
- Publikacja w Delcie: maj 2013
- Publikacja elektroniczna: 30 kwietnia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Zadanie 662 zaproponował pan Paweł Najman z Krakowa. Jest to kontynuacja zadania 654.
Ciąg
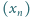 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym
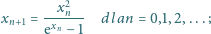
wyraz początkowy
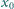 jest dowolną liczbą dodatnią. Obliczyć
granicę
jest dowolną liczbą dodatnią. Obliczyć
granicę
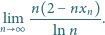

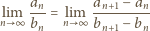
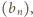 rosnącego do nieskończoności, i dla każdego
ciągu
rosnącego do nieskończoności, i dla każdego
ciągu
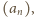 dla którego granica po prawej stronie istnieje.
dla którego granica po prawej stronie istnieje.
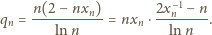
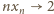 ; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
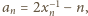
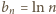 :
:
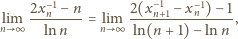
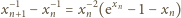
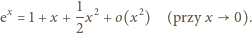
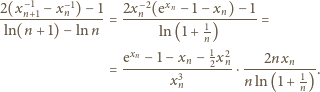
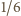 (nieco
dłuższy fragment rozwinięcia
(nieco
dłuższy fragment rozwinięcia
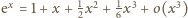 ).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
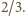 Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
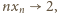 i otrzymujemy
ostatecznie
i otrzymujemy
ostatecznie