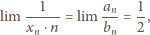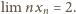Klub 44M - zadania I 2013»Zadanie 654
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2013
- Publikacja w Delcie: styczeń 2013
- Publikacja elektroniczna: 1 stycznia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)
Zadanie 654 zaproponował pan Paweł Najman z Krakowa. Będzie ono miało dalszy ciąg w numerze 5/2013.
Ciąg
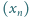 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym

wyraz początkowy
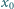 jest dowolną liczbą dodatnią. Obliczyć granicę
jest dowolną liczbą dodatnią. Obliczyć granicę
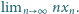

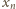 są liczbami dodatnimi. Z nierówności
są liczbami dodatnimi. Z nierówności
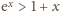 (dla
(dla
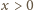 ) wynika, że ciąg
) wynika, że ciąg
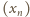 jest malejący –
zatem zbieżny do granicy
jest malejący –
zatem zbieżny do granicy
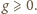 Równanie
Równanie
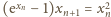 daje
w granicy zależność
daje
w granicy zależność
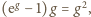 która nie zachodzi dla
żadnej liczby dodatniej
która nie zachodzi dla
żadnej liczby dodatniej
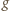 (w myśl tej samej nierówności). Zatem
(w myśl tej samej nierówności). Zatem
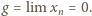
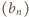 jest ciągiem
rosnącym do nieskończoności, to
jest ciągiem
rosnącym do nieskończoności, to
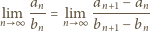
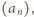 dla którego granica po prawej stronie
istnieje.
dla którego granica po prawej stronie
istnieje.
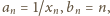 mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
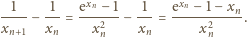
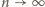 (więc
(więc
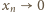 ), ten iloraz dąży do
), ten iloraz dąży do
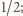 widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
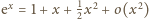 (przy
(przy
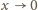 ). Tak więc
). Tak więc