Klub 44M - zadania IX 2012»Zadanie 646
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2012
- Publikacja w Delcie: wrzesień 2012
- Publikacja elektroniczna: 3 września 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (91 KB)
Zadanie 646 zaproponował pan Paweł Najman z Krakowa.
Niech
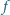 będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
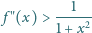 dla
dla
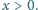 Czy taka funkcja może mieć asymptotę
przy
Czy taka funkcja może mieć asymptotę
przy
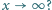

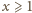 zachodzi nierówność
zachodzi nierówność
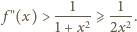
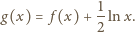
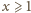 mamy
mamy
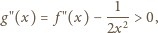
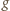 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale
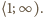 Stąd
wynika, że dla każdej liczby
Stąd
wynika, że dla każdej liczby
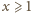 jest spełniona nierówność
jest spełniona nierówność
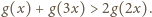 Po podstawieniu wyrażenia definiującego
funkcję
Po podstawieniu wyrażenia definiującego
funkcję
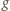 i prostym przekształceniu dostajemy:
i prostym przekształceniu dostajemy:
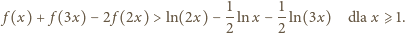
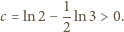
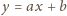 jest asymptotą funkcji
jest asymptotą funkcji
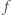 przy
przy
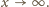 To znaczy, że
To znaczy, że
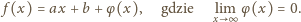
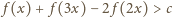
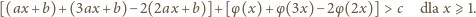
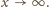 Wniosek: Funkcja
Wniosek: Funkcja
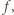 spełniająca podane warunki, nie ma
asymptoty przy
spełniająca podane warunki, nie ma
asymptoty przy