Maksymalna podgrupa właściwa grupy multiplikatywnej liczb wymiernych
dodatnich – tak się w języku algebry nazywa obiekt, którego istnienie należy
rozstrzygnąć. Podamy przykład takiej podgrupy. Każda liczba
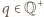 (wymierna dodatnia) daje się przedstawić w postaci
(wymierna dodatnia) daje się przedstawić w postaci
 | (1) |
wykładnik
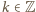 jest wyznaczony jednoznacznie. Określamy zbiór
jest wyznaczony jednoznacznie. Określamy zbiór
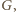 zaliczając doń te liczby powyższej postaci, które mają wykładnik
zaliczając doń te liczby powyższej postaci, które mają wykładnik
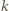 parzysty. Nie wszystkie liczby
parzysty. Nie wszystkie liczby
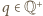 się tu znalazły, więc
się tu znalazły, więc
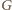 jest podzbiorem właściwym zbioru
jest podzbiorem właściwym zbioru
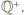 Jest on zamknięty
względem działań mnożenia i dzielenia (tworzy podgrupę grupy
Jest on zamknięty
względem działań mnożenia i dzielenia (tworzy podgrupę grupy
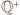 ) –
to jasne. Trzeba jeszcze wykazać, że jeżeli
) –
to jasne. Trzeba jeszcze wykazać, że jeżeli
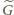 jest podgrupą
grupy
jest podgrupą
grupy
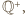 zawierającą
zawierającą
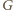 i nie identyczną z
i nie identyczną z
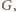 to
to
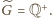
Wybierzmy więc i ustalmy dowolny element
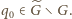 Jest to liczba
postaci (1):
Jest to liczba
postaci (1):
przy czym wykładnik
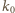 jest nieparzysty. Wszystkie iloczyny
jest nieparzysty. Wszystkie iloczyny
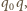 gdzie
gdzie
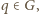 należą do
należą do
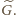 Pisząc
Pisząc
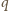 w postaci
(1), z parzystym
w postaci
(1), z parzystym
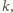 mamy
mamy
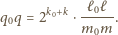 | (2) |
Gdy
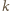 przebiega zbiór wszystkich liczb parzystych,
przebiega zbiór wszystkich liczb parzystych,
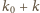 przebiega
zbiór wszystkich liczb nieparzystych. Ponadto każdy ułamek
przebiega
zbiór wszystkich liczb nieparzystych. Ponadto każdy ułamek
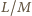 o liczniku
i mianowniku dodatnim nieparzystym możemy uzyskać jako drugi czynnik
przedstawienia (2), biorąc
o liczniku
i mianowniku dodatnim nieparzystym możemy uzyskać jako drugi czynnik
przedstawienia (2), biorąc
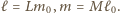
To znaczy, że w zbiorze
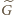 znajdują się wszystkie liczby wymierne
dodatnie z nieparzystą potęgą dwójki. Liczby z parzystą potęgą dwójki, czyli
elementy zbioru
znajdują się wszystkie liczby wymierne
dodatnie z nieparzystą potęgą dwójki. Liczby z parzystą potęgą dwójki, czyli
elementy zbioru
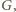 też się w
też się w
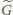 znajdują. Zatem, istotnie,
znajdują. Zatem, istotnie,
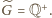
[Nieco ogólniej, można było wziąć dowolne liczby pierwsze
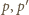 (różne lub nie) i określić
(różne lub nie) i określić
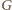 jako zbiór wszystkich ułamków
jako zbiór wszystkich ułamków
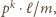 gdzie
gdzie
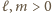 są niepodzielne przez
są niepodzielne przez
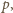 zaś
wykładnik
zaś
wykładnik
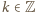 jest podzielny przez
jest podzielny przez
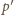 ; takie ułamki również
tworzą maksymalną podgrupę właściwą (w podanym przykładzie przyjęliśmy
; takie ułamki również
tworzą maksymalną podgrupę właściwą (w podanym przykładzie przyjęliśmy
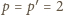 ).]
).]

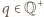 (wymierna dodatnia) daje się przedstawić w postaci
(wymierna dodatnia) daje się przedstawić w postaci

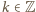 jest wyznaczony jednoznacznie. Określamy zbiór
jest wyznaczony jednoznacznie. Określamy zbiór
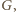 zaliczając doń te liczby powyższej postaci, które mają wykładnik
zaliczając doń te liczby powyższej postaci, które mają wykładnik
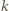 parzysty. Nie wszystkie liczby
parzysty. Nie wszystkie liczby
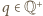 się tu znalazły, więc
się tu znalazły, więc
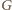 jest podzbiorem właściwym zbioru
jest podzbiorem właściwym zbioru
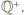 Jest on zamknięty
względem działań mnożenia i dzielenia (tworzy podgrupę grupy
Jest on zamknięty
względem działań mnożenia i dzielenia (tworzy podgrupę grupy
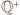 ) –
to jasne. Trzeba jeszcze wykazać, że jeżeli
) –
to jasne. Trzeba jeszcze wykazać, że jeżeli
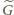 jest podgrupą
grupy
jest podgrupą
grupy
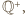 zawierającą
zawierającą
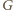 i nie identyczną z
i nie identyczną z
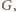 to
to
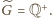
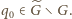 Jest to liczba
postaci (1):
Jest to liczba
postaci (1):
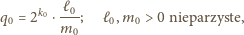
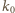 jest nieparzysty. Wszystkie iloczyny
jest nieparzysty. Wszystkie iloczyny
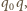 gdzie
gdzie
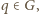 należą do
należą do
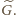 Pisząc
Pisząc
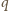 w postaci
(1), z parzystym
w postaci
(1), z parzystym
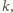 mamy
mamy
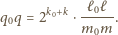
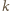 przebiega zbiór wszystkich liczb parzystych,
przebiega zbiór wszystkich liczb parzystych,
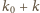 przebiega
zbiór wszystkich liczb nieparzystych. Ponadto każdy ułamek
przebiega
zbiór wszystkich liczb nieparzystych. Ponadto każdy ułamek
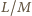 o liczniku
i mianowniku dodatnim nieparzystym możemy uzyskać jako drugi czynnik
przedstawienia (2), biorąc
o liczniku
i mianowniku dodatnim nieparzystym możemy uzyskać jako drugi czynnik
przedstawienia (2), biorąc
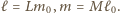
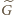 znajdują się wszystkie liczby wymierne
dodatnie z nieparzystą potęgą dwójki. Liczby z parzystą potęgą dwójki, czyli
elementy zbioru
znajdują się wszystkie liczby wymierne
dodatnie z nieparzystą potęgą dwójki. Liczby z parzystą potęgą dwójki, czyli
elementy zbioru
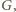 też się w
też się w
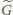 znajdują. Zatem, istotnie,
znajdują. Zatem, istotnie,
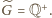
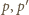 (różne lub nie) i określić
(różne lub nie) i określić
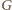 jako zbiór wszystkich ułamków
jako zbiór wszystkich ułamków
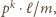 gdzie
gdzie
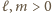 są niepodzielne przez
są niepodzielne przez
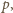 zaś
wykładnik
zaś
wykładnik
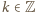 jest podzielny przez
jest podzielny przez
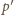 ; takie ułamki również
tworzą maksymalną podgrupę właściwą (w podanym przykładzie przyjęliśmy
; takie ułamki również
tworzą maksymalną podgrupę właściwą (w podanym przykładzie przyjęliśmy
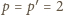 ).]
).]