Klub 44M - zadania IX 2013»Zadanie 666
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2013
- Publikacja w Delcie: wrzesień 2013
- Publikacja elektroniczna: 31 sierpnia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (98 KB)
Zadanie 666 zaproponował pan Witold Bednarek z Łodzi.
Niech
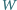 będzie wielomianem stopnia
będzie wielomianem stopnia
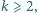 o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
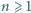 wartość
wartość
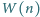 jest
jest
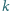 -tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
-tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
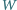 ma postać
ma postać
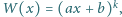 gdzie
gdzie
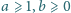 są liczbami całkowitymi.
są liczbami całkowitymi.

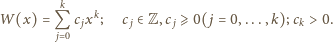
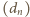 taki,
że
taki,
że
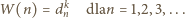
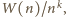 czyli
czyli
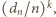 dąży do
dąży do
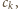 gdy
gdy
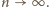 Stąd
Stąd
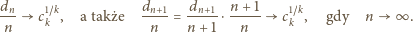
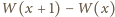 jest wielomianem stopnia
jest wielomianem stopnia
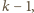 z wyrazem
wiodącym
z wyrazem
wiodącym
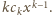 Zatem
Zatem
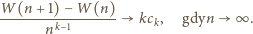
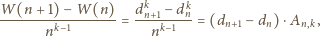
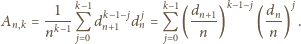
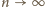 mamy
mamy
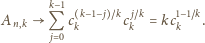
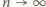
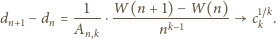
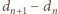 przedstawia więc ciąg liczb całkowitych, który jest
zbieżny – taki ciąg jest od pewnego miejsca stały. Oznaczając
przedstawia więc ciąg liczb całkowitych, który jest
zbieżny – taki ciąg jest od pewnego miejsca stały. Oznaczając
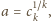 mamy
zatem
mamy
zatem
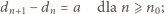
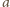 jest całkowita oraz dodatnia.
jest całkowita oraz dodatnia.
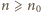 uzyskujemy równość
uzyskujemy równość
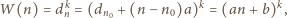
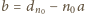 jest liczbą całkowitą.
jest liczbą całkowitą.
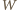 jest wielomianem
jest wielomianem
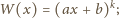
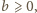 skoro (z założenia)
współczynniki
skoro (z założenia)
współczynniki
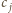 wielomianu
wielomianu
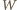 są nieujemne, zaś
są nieujemne, zaś