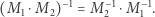Zliczamy podciągi
Zaczniemy od takiego zadania: dla danego  -literowego słowa
-literowego słowa  chcemy znaleźć liczbę jego różnych podciągów. Innymi słowy, chcemy odpowiedzieć na pytanie, ile różnych słów możemy uzyskać poprzez wykreślanie niektórych liter ze słowa
chcemy znaleźć liczbę jego różnych podciągów. Innymi słowy, chcemy odpowiedzieć na pytanie, ile różnych słów możemy uzyskać poprzez wykreślanie niektórych liter ze słowa  Dla przykładu rozważmy słowo ABAA. Ma ono dokładnie 10 różnych podciągów: słowo puste, A, B, AA, AB, BA, AAA, ABA, BAA oraz ABAA. Dla uproszczenia będziemy rozważać słowa złożone z liter A i B, ale nasze rozwiązania będą działać dla dowolnego
Dla przykładu rozważmy słowo ABAA. Ma ono dokładnie 10 różnych podciągów: słowo puste, A, B, AA, AB, BA, AAA, ABA, BAA oraz ABAA. Dla uproszczenia będziemy rozważać słowa złożone z liter A i B, ale nasze rozwiązania będą działać dla dowolnego  -literowego alfabetu.
-literowego alfabetu. 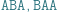
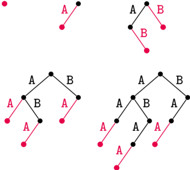
Rys. 1. Konstrukcja drzewa trie dla kolejnych prefiksów słowa ABAA. Krawędzie dodawane w kolejnych krokach zaznaczono kolorem; wynikowe drzewo ma 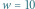 węzłów
węzłów
Zaczniemy od algorytmu, który będzie konstruował możliwe do uzyskania podciągi dla kolejnych prefiksów słowa  (Rys. 1). Wygodnie jest trzymać te podciągi na drzewie, w którym krawędzie są etykietowane literami, a każda ścieżka od korzenia do dowolnego węzła odpowiada jednemu podciągowi (czyli na tzw. drzewie trie). Tak więc liczba węzłów
(Rys. 1). Wygodnie jest trzymać te podciągi na drzewie, w którym krawędzie są etykietowane literami, a każda ścieżka od korzenia do dowolnego węzła odpowiada jednemu podciągowi (czyli na tzw. drzewie trie). Tak więc liczba węzłów 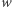 tego drzewa będzie oznaczała liczbę różnych podciągów (włączając korzeń drzewa odpowiadający podciągowi pustemu).
tego drzewa będzie oznaczała liczbę różnych podciągów (włączając korzeń drzewa odpowiadający podciągowi pustemu).
Przypuśćmy, że skonstruowaliśmy drzewo dla prefiksu 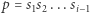 i chcemy dodać kolejną literę
i chcemy dodać kolejną literę  aby uzyskać drzewo dla prefiksu
aby uzyskać drzewo dla prefiksu  Wszystkie podciągi z
Wszystkie podciągi z 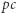 będą albo podciągami występującymi już w
będą albo podciągami występującymi już w 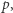 albo tymi samymi podciągami rozszerzonymi o literę
albo tymi samymi podciągami rozszerzonymi o literę 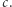 Tak więc, gdy w drzewie dla
Tak więc, gdy w drzewie dla 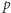 do każdego węzła dodamy krawędź o etykiecie
do każdego węzła dodamy krawędź o etykiecie 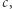 uzyskamy drzewo dla
uzyskamy drzewo dla 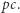 Może się zdarzyć, że w niektórych węzłach taka krawędź już istniała - oznacza to, że odpowiadający podciąg już występował w
Może się zdarzyć, że w niektórych węzłach taka krawędź już istniała - oznacza to, że odpowiadający podciąg już występował w 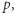 zatem nie należy go dodawać ponownie.
zatem nie należy go dodawać ponownie.
Taki algorytm, choć poprawny, ma złożoność wykładniczą względem 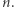 Istotnie, słowo złożone z
Istotnie, słowo złożone z  różnych liter ma
różnych liter ma 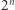 podciągów. Ale dla dwuliterowego alfabetu nie jest dużo lepiej: słowo
podciągów. Ale dla dwuliterowego alfabetu nie jest dużo lepiej: słowo 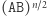 (AB powtórzone
(AB powtórzone 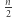 razy) ma więcej niż
razy) ma więcej niż 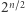 podciągów (w szczególności zawiera wszystkie możliwe
podciągów (w szczególności zawiera wszystkie możliwe 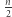 -literowe słowa jako podciągi).
-literowe słowa jako podciągi).
Okazuje się, że aby znaleźć liczbę podciągów, nie musimy trzymać w pamięci całego drzewa. Niech 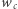 oznacza liczbę węzłów drzewa, z których wychodzi krawędź z literą
oznacza liczbę węzłów drzewa, z których wychodzi krawędź z literą  (jest to też po prostu liczba krawędzi z etykietą
(jest to też po prostu liczba krawędzi z etykietą  ). Gdy dodajemy literę
). Gdy dodajemy literę  dodajemy nową krawędź do dokładnie
dodajemy nową krawędź do dokładnie 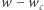 węzłów, a zatem zwiększamy sumaryczną liczbę węzłów (tym samym liczbę podciągów) z
węzłów, a zatem zwiększamy sumaryczną liczbę węzłów (tym samym liczbę podciągów) z  na
na 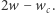 Ponadto zwiększamy liczbę krawędzi z etykietą
Ponadto zwiększamy liczbę krawędzi z etykietą  z
z 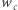 do
do 
Wystarczy więc, że będziemy trzymali w pamięci wektor  początkowo równy
początkowo równy  Gdy dodajemy nową literę A, to zastępujemy ten wektor przez
Gdy dodajemy nową literę A, to zastępujemy ten wektor przez 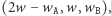 a dla litery B przez wektor
a dla litery B przez wektor  Ponieważ zawsze zmieniamy tylko dwie współrzędne wektora, to dostajemy rozwiązanie o złożoności czasowej
Ponieważ zawsze zmieniamy tylko dwie współrzędne wektora, to dostajemy rozwiązanie o złożoności czasowej 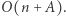

W konkursach programistycznych panuje moda na utrudnianie zadań z ciągami przez rozważanie wielu zapytań o fragmenty słowa. Spróbujmy zmierzyć się z taką wersją zadania. Dostajemy zatem  zapytań, każde postaci
zapytań, każde postaci  o liczbę różnych podciągów dla fragmentu
o liczbę różnych podciągów dla fragmentu  Przy czym
Przy czym  jest duże, więc nie możemy sobie pozwolić na uruchomienie algorytmu liniowego dla każdego zapytania oddzielnie.
jest duże, więc nie możemy sobie pozwolić na uruchomienie algorytmu liniowego dla każdego zapytania oddzielnie.
W algorytmie dla jednego zapytania utrzymujemy wektor 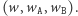 Ponieważ współczynniki nowego wektora (po dodaniu litery) są kombinacjami liniowymi współczynników oryginalnego wektora, więc możemy zamianę wektora zastąpić mnożeniem go z prawej strony przez jedną z poniższych macierzy:
Ponieważ współczynniki nowego wektora (po dodaniu litery) są kombinacjami liniowymi współczynników oryginalnego wektora, więc możemy zamianę wektora zastąpić mnożeniem go z prawej strony przez jedną z poniższych macierzy:
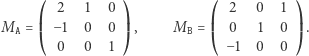 |
Nadużywając nieco notacji, oznaczmy przez  macierz odpowiadającą
macierz odpowiadającą 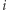 -tej literze słowa
-tej literze słowa 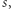 czyli
czyli  Zaczynając od wektora
Zaczynając od wektora  mnożymy go przez kolejne wartości
mnożymy go przez kolejne wartości 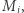 uzyskując na końcu wektor
uzyskując na końcu wektor 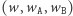 dla całego słowa. Pomnożywszy go skalarnie przez
dla całego słowa. Pomnożywszy go skalarnie przez 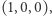 dostajemy wartość
dostajemy wartość 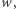 czyli szukaną liczbę podciągów. Ponieważ macierze są rozmiarów
czyli szukaną liczbę podciągów. Ponieważ macierze są rozmiarów 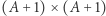 i umiemy pomnożyć dwie takie macierze w czasie
i umiemy pomnożyć dwie takie macierze w czasie 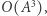 to cały algorytm, sprowadzający się do obliczenia wzoru
to cały algorytm, sprowadzający się do obliczenia wzoru
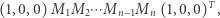 |
zadziała w czasie 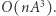 Jest to istotnie gorsza złożoność, niż mieliśmy wcześniej, ale przedstawienie obliczeń w postaci macierzowej daje nam większą elastyczność. Obliczenie odpowiedzi dla fragmentu
Jest to istotnie gorsza złożoność, niż mieliśmy wcześniej, ale przedstawienie obliczeń w postaci macierzowej daje nam większą elastyczność. Obliczenie odpowiedzi dla fragmentu 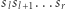 wymaga bowiem przemnożenia macierzy
wymaga bowiem przemnożenia macierzy 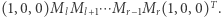 Ponieważ mnożenie macierzy jest operacją łączną, więc w tym celu możemy użyć struktury danych zwanej drzewem przedziałowym. W liściach drzewa będziemy trzymać macierze
Ponieważ mnożenie macierzy jest operacją łączną, więc w tym celu możemy użyć struktury danych zwanej drzewem przedziałowym. W liściach drzewa będziemy trzymać macierze 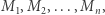 a w węzłach wewnętrznych przemnożone macierze z dzieci. Dzięki temu będziemy mogli odpytywać o iloczyn macierzy dla dowolnego fragmentu w czasie
a w węzłach wewnętrznych przemnożone macierze z dzieci. Dzięki temu będziemy mogli odpytywać o iloczyn macierzy dla dowolnego fragmentu w czasie 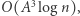 gdyż dzielimy go na
gdyż dzielimy go na 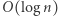 przedziałów bazowych, których macierze mnożymy w czasie
przedziałów bazowych, których macierze mnożymy w czasie 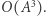 Z kolei sama konstrukcja drzewa zajmie czas
Z kolei sama konstrukcja drzewa zajmie czas 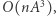 więc algorytm będzie działał w sumarycznej złożoności czasowej
więc algorytm będzie działał w sumarycznej złożoności czasowej 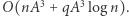
Można ją jeszcze trochę przyspieszyć, korzystając ze standardowej sztuczki dla zapytań o iloczyny macierzy. Tak naprawdę nie pytamy się o całą macierz, a o jeden z jej elementów (dlatego mnożymy obustronnie przez wektor). Ponieważ mnożenie macierzy przez wektor działa w czasie  jest więc szybsze niż mnożenie macierzy przez macierz (i daje w wyniku wektor), możemy zatem macierze dla przedziałów bazowych od razu domnażać do jednego z tych wektorów. Tym sposobem algorytm będzie działał w czasie
jest więc szybsze niż mnożenie macierzy przez macierz (i daje w wyniku wektor), możemy zatem macierze dla przedziałów bazowych od razu domnażać do jednego z tych wektorów. Tym sposobem algorytm będzie działał w czasie 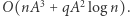
Własność mnożenia macierzy, którą wykorzystujemy w drzewie przedziałowym, to łączność. Gdyby dodatkowo nasze macierze 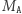 i
i 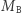 były odwracalne, to zamiast drzewa przedziałowego moglibyśmy wykorzystać zwykłe sumy (a właściwie iloczyny) prefiksowe. Jeśli przyjmiemy oznaczenie
były odwracalne, to zamiast drzewa przedziałowego moglibyśmy wykorzystać zwykłe sumy (a właściwie iloczyny) prefiksowe. Jeśli przyjmiemy oznaczenie 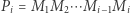 oraz
oraz 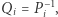 to wtedy
to wtedy  oraz
oraz
 |
Niestety, nie wszystkie macierze są odwracalne. Ale popatrzmy na macierz  jako przekształcającą wektor
jako przekształcającą wektor  na wektor
na wektor  gdzie
gdzie  i
i 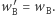 Gdybyśmy dostali wektor
Gdybyśmy dostali wektor  to czy umielibyśmy na jego podstawie odtworzyć wektor
to czy umielibyśmy na jego podstawie odtworzyć wektor  Odpowiedź jest twierdząca - proste przekształcenia prowadzą do wzoru
Odpowiedź jest twierdząca - proste przekształcenia prowadzą do wzoru  i
i  Są to również przekształcenia liniowe, więc możemy je zapisać w formie macierzy, która musi być zatem macierzą odwrotną do
Są to również przekształcenia liniowe, więc możemy je zapisać w formie macierzy, która musi być zatem macierzą odwrotną do  (tak samo odwracamy macierz
(tak samo odwracamy macierz  ):
):
 |
Możemy więc w czasie  wyznaczyć wszystkie
wyznaczyć wszystkie  biorąc
biorąc  Macierz odwrotną
Macierz odwrotną 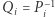 możemy również obliczyć w czasie
możemy również obliczyć w czasie 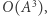 ale jest to bardziej kłopotliwe niż mnożenie. Aby tego uniknąć, wyznaczymy
ale jest to bardziej kłopotliwe niż mnożenie. Aby tego uniknąć, wyznaczymy 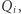 korzystając ze wzoru
korzystając ze wzoru
 |
Teraz jedno zapytanie będzie działać w czasie 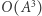 lub nawet w czasie
lub nawet w czasie 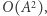 bo dla wyniku potrzebujemy wykonać mnożenie
bo dla wyniku potrzebujemy wykonać mnożenie 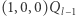 oraz mnożenie
oraz mnożenie  a następnie pomnożyć skalarnie uzyskane wektory. Ale jeśli przyjrzymy się temu wzorowi bliżej, to tak naprawdę mnożymy w nim pierwszy wiersz macierzy
a następnie pomnożyć skalarnie uzyskane wektory. Ale jeśli przyjrzymy się temu wzorowi bliżej, to tak naprawdę mnożymy w nim pierwszy wiersz macierzy 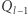 przez pierwszą kolumnę macierzy
przez pierwszą kolumnę macierzy  zatem możemy to bezpośrednio zrobić w czasie
zatem możemy to bezpośrednio zrobić w czasie 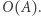 Dostajemy zatem algorytm o złożoności czasowej
Dostajemy zatem algorytm o złożoności czasowej 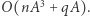
Przypomnijmy, że zaczęliśmy od rekurencji liniowej, którą zapisaliśmy w postaci macierzy, aby skorzystać z ich własności (łączności dla drzewa przedziałowego i istnienia odwrotności dla iloczynów prefiksowych). Zauważmy, że o ile w drzewie przedziałowym potrzebowaliśmy umieć mnożyć dowolne macierze, to w algorytmie sum prefiksowych wystarczy nam domnażanie przez macierze 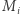 oraz
oraz 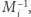 więc znowu możemy skorzystać z faktu, są one szczególnej postaci. Domnażanie macierzy
więc znowu możemy skorzystać z faktu, są one szczególnej postaci. Domnażanie macierzy  przez
przez 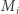 modyfikuje jedynie dwie kolumny macierzy
modyfikuje jedynie dwie kolumny macierzy 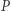 (przykładowo dla
(przykładowo dla  na drugą kolumnę kopiujemy pierwszą, a pierwszą mnożymy przez 2 i odejmujemy drugą). Zatem możemy skopiować macierz
na drugą kolumnę kopiujemy pierwszą, a pierwszą mnożymy przez 2 i odejmujemy drugą). Zatem możemy skopiować macierz 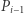 do macierzy
do macierzy 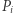 w czasie
w czasie 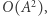 a następnie zrobić uaktualnienie dwóch kolumn w czasie
a następnie zrobić uaktualnienie dwóch kolumn w czasie 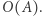 (Analogicznie dla macierzy
(Analogicznie dla macierzy 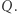 ) Tak więc fazę obliczeń wstępnych możemy zrealizować w czasie
) Tak więc fazę obliczeń wstępnych możemy zrealizować w czasie 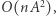 co da nam algorytm o złożoności
co da nam algorytm o złożoności 
Czas na ostatnią obserwację: wcale nie musimy pracowicie kopiować całych macierzy. Ponieważ z macierzy 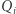 potrzebujemy jedynie pierwszego wiersza, a z macierzy
potrzebujemy jedynie pierwszego wiersza, a z macierzy 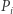 jedynie pierwszej kolumny, zatem wystarczy te macierze modyfikować w miejscu (czyli nadpisując nieaktualne wartości nowymi w tym samym miejscu), a kopiować jedynie potrzebne wiersze i kolumny, co zajmie czas
jedynie pierwszej kolumny, zatem wystarczy te macierze modyfikować w miejscu (czyli nadpisując nieaktualne wartości nowymi w tym samym miejscu), a kopiować jedynie potrzebne wiersze i kolumny, co zajmie czas 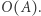 Zatem ostatecznie dostajemy rozwiązanie o złożoności czasowej
Zatem ostatecznie dostajemy rozwiązanie o złożoności czasowej 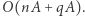
 węzłów
węzłów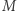 jest odwracalna, jeśli istnieje taka macierz
jest odwracalna, jeśli istnieje taka macierz 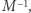 że iloczyny
że iloczyny 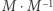 oraz
oraz  są równe macierzy identycznościowej.
są równe macierzy identycznościowej.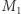 i
i 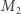 mamy
mamy