Informatyczny kącik olimpijski
Yet Another Substring Reverse
Tym razem omówimy zadanie Yet Another Substring Reverse, które pojawiło się na portalu www.codeforces.com.
Zadanie. Dane jest słowo 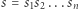 o długości
o długości 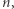 zawierające wystąpienia części liter alfabetu angielskiego
zawierające wystąpienia części liter alfabetu angielskiego 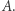 W słowie
W słowie  należy odwrócić jedno podsłowo, tzn. zastąpić je zapisem od prawej do lewej, aby otrzymać możliwie najdłuższe różnorodne podsłowo, czyli takie, które nie zawiera powtórzeń liter. Jaka jest długość najdłuższego różnorodnego podsłowa, które można uzyskać? Przykładowo dla
należy odwrócić jedno podsłowo, tzn. zastąpić je zapisem od prawej do lewej, aby otrzymać możliwie najdłuższe różnorodne podsłowo, czyli takie, które nie zawiera powtórzeń liter. Jaka jest długość najdłuższego różnorodnego podsłowa, które można uzyskać? Przykładowo dla 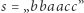 wynikiem jest 3. Po odwróceniu fragmentu od trzeciej do szóstej litery otrzymujemy
wynikiem jest 3. Po odwróceniu fragmentu od trzeciej do szóstej litery otrzymujemy 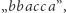 którego najdłuższy różnorodny fragment to
którego najdłuższy różnorodny fragment to 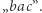
Niech 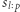 oznacza podsłowo
oznacza podsłowo 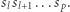
Na samym początku zauważmy, że długość różnorodnego podsłowa nie przekroczy 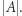
Najdłuższe różnorodne podsłowo 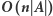
Załóżmy przez chwilę, że nie wykonujemy odwrócenia i chcemy znaleźć długość najdłuższego różnorodnego podsłowa. Dla każdej pozycji początkowej wyznaczmy najdłuższe różnorodne podsłowo, które się w niej zaczyna. Formalnie dla ustalonego 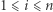 znajdźmy takie największe
znajdźmy takie największe 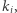 że
że 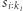 jest różnorodne. Zacznijmy od jednoliterowego podsłowa
jest różnorodne. Zacznijmy od jednoliterowego podsłowa 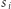 i rozszerzajmy je o kolejne litery, dopóki nie nastąpi powtórzenie. Do sprawdzania, czy jakaś litera wystąpiła wcześniej, można wykorzystać tablicę zliczającą, którą po każdym rozszerzeniu aktualizujemy. Opisane rozwiązanie działa w czasie
i rozszerzajmy je o kolejne litery, dopóki nie nastąpi powtórzenie. Do sprawdzania, czy jakaś litera wystąpiła wcześniej, można wykorzystać tablicę zliczającą, którą po każdym rozszerzeniu aktualizujemy. Opisane rozwiązanie działa w czasie 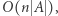 gdyż od każdej pozycji początkowej wykonamy co najwyżej
gdyż od każdej pozycji początkowej wykonamy co najwyżej 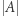 rozszerzeń w prawo.
rozszerzeń w prawo.
Najdłuższe różnorodne podsłowo 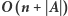
W tym rozwiązaniu, podobnie jak wcześniej, dla każdej pozycji 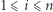 chcemy wyznaczyć takie największe
chcemy wyznaczyć takie największe 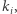 że
że 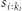 jest różnorodne. Skorzystajmy z metody gąsienicy. Otóż, tym razem nie będziemy dla każdej pozycji początkowej rozpoczynali przeszukiwania od słów jednoliterowych. Zauważmy, że jeśli
jest różnorodne. Skorzystajmy z metody gąsienicy. Otóż, tym razem nie będziemy dla każdej pozycji początkowej rozpoczynali przeszukiwania od słów jednoliterowych. Zauważmy, że jeśli 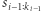 jest różnorodne, to również
jest różnorodne, to również 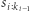 jest różnorodne. Zatem nie ma potrzeby sprawdzania słów, które kończą się wcześniej niż
jest różnorodne. Zatem nie ma potrzeby sprawdzania słów, które kończą się wcześniej niż 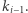 Do sprawdzania powtórzeń wykorzystujemy tablicę zliczającą. Przy rozszerzaniu słowa z prawej strony dodajemy literę, a przy przejściu do kolejnej pozycji początkowej usuwamy literę z tablicy zliczającej. Rozwiązanie działa w czasie
Do sprawdzania powtórzeń wykorzystujemy tablicę zliczającą. Przy rozszerzaniu słowa z prawej strony dodajemy literę, a przy przejściu do kolejnej pozycji początkowej usuwamy literę z tablicy zliczającej. Rozwiązanie działa w czasie 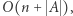 gdyż każda litera zostanie dokładnie raz dodana i raz usunięta z tablicy zliczającej.
gdyż każda litera zostanie dokładnie raz dodana i raz usunięta z tablicy zliczającej.
Rozwiązanie 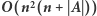
Opisaliśmy metody znajdowania najdłuższego różnorodnego podsłowa, zatem możemy przejść do pierwszego rozwiązania zadania. Rozważmy odwrócenie każdego z 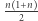 podsłów. Dla każdego przypadku znajdźmy najdłuższe różnorodne podsłowo za pomocą jednej z wyżej opisanych metod i wybierzmy najlepszy wynik. W zależności od wykorzystanej metody otrzymamy rozwiązanie
podsłów. Dla każdego przypadku znajdźmy najdłuższe różnorodne podsłowo za pomocą jednej z wyżej opisanych metod i wybierzmy najlepszy wynik. W zależności od wykorzystanej metody otrzymamy rozwiązanie 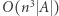 lub
lub 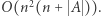
Rozwiązanie 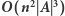
Zauważmy, że możemy zredukować zadanie do znalezienia dwóch różnorodnych podsłów, które mają rozłączne zbiory liter oraz największą sumaryczną długość. Formalny dowód tego faktu pozostawiamy Czytelnikowi, a teraz pokażemy, jak dwa podsłowa, 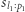 oraz
oraz 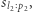 niemające wspólnych liter umieścić obok siebie za pomocą jednego odwrócenia. Załóżmy bez straty ogólności, że
niemające wspólnych liter umieścić obok siebie za pomocą jednego odwrócenia. Załóżmy bez straty ogólności, że 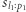 występuje na lewo od
występuje na lewo od 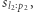 wówczas należy odwrócić
wówczas należy odwrócić 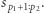 Teraz
Teraz 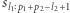 jest różnorodne.
jest różnorodne.
Znajdźmy wszystkie różnorodne podsłowa, których jest 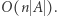 Następnie rozważmy każdą z
Następnie rozważmy każdą z 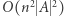 par takich podsłów. Jeśli podsłowa mają rozłączne zbiory liter, wtedy razem tworzą różnorodne podsłowo. Sprawdzenie, czy zbiory liter są rozłączne, możemy wykonać metodą zliczenia w czasie
par takich podsłów. Jeśli podsłowa mają rozłączne zbiory liter, wtedy razem tworzą różnorodne podsłowo. Sprawdzenie, czy zbiory liter są rozłączne, możemy wykonać metodą zliczenia w czasie 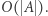 Spośród par tworzących różnorodne podsłowa wybieramy tę, której sumaryczna długość fragmentów jest największa. Otrzymaliśmy rozwiązanie o złożoności czasowej
Spośród par tworzących różnorodne podsłowa wybieramy tę, której sumaryczna długość fragmentów jest największa. Otrzymaliśmy rozwiązanie o złożoności czasowej 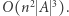
Rozwiązanie 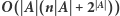
Zauważmy, że kolejność liter w podsłowie nie ma znaczenia, zatem każde różnorodne podsłowo możemy rozważać jako zbiór liter. Spośród wszystkich podsłów o długości co najwyżej 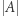 znajdźmy te, które są różnorodne, i zbiory ich liter oznaczmy jako zbiór
znajdźmy te, które są różnorodne, i zbiory ich liter oznaczmy jako zbiór 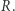 Przykładowo dla
Przykładowo dla 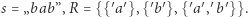 Wyznaczenie
Wyznaczenie 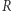 zajmuje czas
zajmuje czas 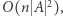 zaś moc
zaś moc 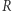 wynosi co najwyżej
wynosi co najwyżej 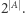 Zadanie redukuje się teraz do znalezienia dwóch rozłącznych zbiorów w
Zadanie redukuje się teraz do znalezienia dwóch rozłącznych zbiorów w 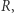 których suma ma największą moc.
których suma ma największą moc.
Dla każdego zbioru 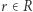 znajdźmy taki zbiór
znajdźmy taki zbiór 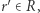 że
że 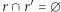 oraz
oraz 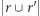 jest maksymalne. Innymi słowy dla każdego zbioru znajdźmy inny zbiór, który tworzy z nim najlepszy wynik. Wówczas odpowiedzią w zadaniu jest maksimum z rozważonych przypadków. Niech
jest maksymalne. Innymi słowy dla każdego zbioru znajdźmy inny zbiór, który tworzy z nim najlepszy wynik. Wówczas odpowiedzią w zadaniu jest maksimum z rozważonych przypadków. Niech ![W[a]](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/5x-0071e2c635228f2698fefe9eb82fb33c83678b3f-im-33,33,33-FF,FF,FF.gif) dla każdego
dla każdego 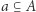 oznacza moc największego takiego zbioru
oznacza moc największego takiego zbioru 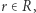 że
że 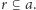 Teraz
Teraz 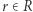 tworzy najdłuższe różnorodne podsłowo o długości
tworzy najdłuższe różnorodne podsłowo o długości ![- | r + W[r],](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/10x-0071e2c635228f2698fefe9eb82fb33c83678b3f-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 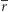 oznacza dopełnienie
oznacza dopełnienie 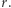
Pozostało nam jeszcze wyznaczyć wartości 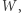 które będziemy obliczali w kolejności niemalejących mocy zbiorów. Załóżmy, że obliczamy
które będziemy obliczali w kolejności niemalejących mocy zbiorów. Załóżmy, że obliczamy ![|W[a]](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/2x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) i mamy obliczone
i mamy obliczone ![|W[b]](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/3x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) dla wszystkich
dla wszystkich 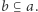 Jeśli
Jeśli 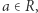 wówczas
wówczas ![|W[a] = a .](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/6x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku
W przeciwnym przypadku ![W[a] < a ,](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/7x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) czyli największy podzbiór
czyli największy podzbiór  należący jednocześnie do
należący jednocześnie do 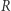 nie zawiera jakiegoś elementu
nie zawiera jakiegoś elementu 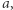 zatem
zatem ![W[a] = maxe> aW[a ∖ e] .](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/11x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) Obliczenie
Obliczenie ![W[a]](/math/temat/informatyka/algorytmy/2020/05/30/yet-another-substring-reverse/12x-3057d6e857cd3d9ba13fb65524732c8409621a2d-im-33,33,33-FF,FF,FF.gif) zajmuje czas
zajmuje czas 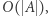 wartości tablicy
wartości tablicy 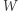 jest
jest 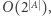 zatem czas potrzebny do obliczenia
zatem czas potrzebny do obliczenia 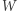 wynosi
wynosi 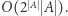 Całe rozwiązanie działa w czasie
Całe rozwiązanie działa w czasie