Informatyczny kącik olimpijski
Theater Tickets
Tym razem omówimy zadanie "Theater Tickets", które pojawiło się w konkursie Zinc 2018 organizowanym przez firmę Codility.
Zadanie. Dany jest 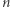 -elementowy ciąg liczb naturalnych
-elementowy ciąg liczb naturalnych 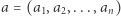 z przedziału od 1 do
z przedziału od 1 do 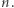 Oblicz, ile różnych trzyelementowych podciągów występuje w ciągu
Oblicz, ile różnych trzyelementowych podciągów występuje w ciągu 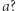 Dwa podciągi uznajemy za różne, jeśli różnią się na przynajmniej jednej pozycji. Przykładowo
Dwa podciągi uznajemy za różne, jeśli różnią się na przynajmniej jednej pozycji. Przykładowo 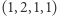 ma trzy różne podciągi:
ma trzy różne podciągi: 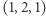 (występujący dwa razy),
(występujący dwa razy), 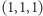 (występujący raz) oraz
(występujący raz) oraz 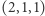 (występujący raz).
(występujący raz).
Niech 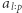 oznacza podsłowo
oznacza podsłowo 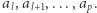
Rozwiązanie 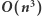
Pierwsze rozwiązanie będzie polegało na prostym zliczeniu podciągów trzyelementowych. Zauważmy, że wszystkich trzyelementowych ciągów o wartościach z przedziału ![|[1;n]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/2x-da3367ea9b643d3d83f08c58bbf35ee33977a754-im-33,33,33-FF,FF,FF.gif) jest
jest 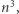 gdyż każdy z trzech elementów można wybrać na
gdyż każdy z trzech elementów można wybrać na 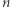 sposobów. Niech
sposobów. Niech ![|T[x][y][z] = 1,](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/5x-da3367ea9b643d3d83f08c58bbf35ee33977a754-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 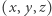 jest podciągiem
jest podciągiem  oraz
oraz ![T [x][y][z] = 0](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/8x-da3367ea9b643d3d83f08c58bbf35ee33977a754-im-33,33,33-FF,FF,FF.gif) w przeciwnym przypadku. Aby uzupełnić tablicę zliczającą
w przeciwnym przypadku. Aby uzupełnić tablicę zliczającą 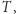 wystarczy dla każdej trójki indeksów
wystarczy dla każdej trójki indeksów 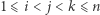 zaktualizować
zaktualizować ![T[ai][a j][ak] = 1.](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/11x-da3367ea9b643d3d83f08c58bbf35ee33977a754-im-33,33,33-FF,FF,FF.gif) Ta faza zajmuje czas
Ta faza zajmuje czas 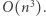 Wynikiem jest liczba komórek tablicy zliczającej
Wynikiem jest liczba komórek tablicy zliczającej 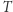 o wartości 1. Rozwiązanie działa w czasie i pamięci
o wartości 1. Rozwiązanie działa w czasie i pamięci 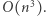
Rozwiązanie 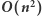
Policzmy dla każdego prefiksu, ile zawiera on różnych dwuelementowych podciągów. Niech ![P 2[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/2x-76bf8bf10110fb97678999648c9166fb97fd6da6-im-33,33,33-FF,FF,FF.gif) oznacza tę wartość dla
oznacza tę wartość dla 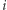 -elementowego prefiksu
-elementowego prefiksu 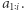 Wyniki będziemy obliczali od najkrótszych do najdłuższych prefiksów. Oczywiście
Wyniki będziemy obliczali od najkrótszych do najdłuższych prefiksów. Oczywiście ![|P2[1] = 0.](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/5x-76bf8bf10110fb97678999648c9166fb97fd6da6-im-33,33,33-FF,FF,FF.gif) Zastanówmy się zatem, jak wyznaczyć
Zastanówmy się zatem, jak wyznaczyć ![|P2[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/6x-76bf8bf10110fb97678999648c9166fb97fd6da6-im-33,33,33-FF,FF,FF.gif) dla
dla 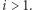 Otóż
Otóż ![P2[i] = P 2[i− 1] +l,](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/8x-76bf8bf10110fb97678999648c9166fb97fd6da6-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 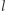 oznacza liczbę takich dwuelementowych podciągów, które nie występują w
oznacza liczbę takich dwuelementowych podciągów, które nie występują w 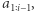 ale występują w
ale występują w 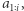 czyli takich, których drugim elementem jest
czyli takich, których drugim elementem jest 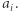 Rozważmy więc takie dwuelementowe podciągi
Rozważmy więc takie dwuelementowe podciągi 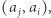 że
że 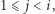 i zliczmy te, które nie występują w
i zliczmy te, które nie występują w 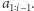 Aby sprawdzić, które dwuelementowe podciągi wystąpiły wcześniej, można, podobnie jak w poprzednim rozwiązaniu, skorzystać z tablicy zliczającej. Wynik dla każdego prefiksu liczymy w czasie
Aby sprawdzić, które dwuelementowe podciągi wystąpiły wcześniej, można, podobnie jak w poprzednim rozwiązaniu, skorzystać z tablicy zliczającej. Wynik dla każdego prefiksu liczymy w czasie 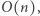 prefiksów jest
prefiksów jest 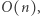 zatem
zatem 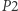 obliczamy w czasie
obliczamy w czasie 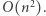
Przejdźmy teraz do wyznaczenia liczby różnych trzyelementowych podciągów 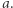 Na początku dla każdej wartości od 1 do
Na początku dla każdej wartości od 1 do 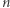 zapamiętajmy numer ostatniej pozycji, na której ta wartość występuje w
zapamiętajmy numer ostatniej pozycji, na której ta wartość występuje w 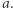 Niech
Niech ![|ost[x]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/4x-d9bb8215d2b50afb214d1f60c5179f2d61ee9e9b-im-33,33,33-FF,FF,FF.gif) oznacza takie największe
oznacza takie największe 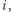 że
że 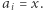 Podciągi będziemy zliczali grupami, biorąc pod uwagę wartość ostatniego elementu. Otóż policzymy, ile jest podciągów, których ostatni element to odpowiednio
Podciągi będziemy zliczali grupami, biorąc pod uwagę wartość ostatniego elementu. Otóż policzymy, ile jest podciągów, których ostatni element to odpowiednio 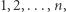 a na koniec zsumujemy te wyniki. Zastanówmy się, jak dla ustalonego
a na koniec zsumujemy te wyniki. Zastanówmy się, jak dla ustalonego  wyznaczyć liczbę różnych podciągów w
wyznaczyć liczbę różnych podciągów w  postaci
postaci 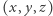 dla
dla 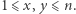 Jeśli
Jeśli  nie występuje w
nie występuje w 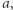 to nie ma takich podciągów. W przeciwnym przypadku weźmy ostatnie wystąpienie
to nie ma takich podciągów. W przeciwnym przypadku weźmy ostatnie wystąpienie  w
w 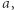 które znajduje się na pozycji
które znajduje się na pozycji ![|ost[z].](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/16x-d9bb8215d2b50afb214d1f60c5179f2d61ee9e9b-im-33,33,33-FF,FF,FF.gif) Trzeci element mamy ustalony, zaś dwa pierwsze elementy możemy wybrać na
Trzeci element mamy ustalony, zaś dwa pierwsze elementy możemy wybrać na ![|P2[ost[z]− 1]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/17x-d9bb8215d2b50afb214d1f60c5179f2d61ee9e9b-im-33,33,33-FF,FF,FF.gif) sposobów, co jest równe liczbie różnych trzyelementowych podciągów kończących się liczbą
sposobów, co jest równe liczbie różnych trzyelementowych podciągów kończących się liczbą 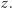 Całkowita liczba trzyelementowych podciągów to
Całkowita liczba trzyelementowych podciągów to ![n |P z 1P 2[ost[z] − 1],](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/19x-d9bb8215d2b50afb214d1f60c5179f2d61ee9e9b-im-33,33,33-FF,FF,FF.gif) co możemy obliczyć w
co możemy obliczyć w 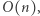 znając
znając 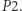 Natomiast całe rozwiązanie działa w czasie i pamięci
Natomiast całe rozwiązanie działa w czasie i pamięci 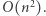
Rozwiązanie 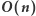
Spróbujmy przyspieszyć pierwszą fazę poprzedniego rozwiązania (obliczanie 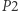 ). Na początku dla każdego prefiksu policzmy, ile zawiera on różnych wartości (podciągów jednoelementowych). Niech
). Na początku dla każdego prefiksu policzmy, ile zawiera on różnych wartości (podciągów jednoelementowych). Niech ![|P1[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/3x-edc0a1341bd2106f6e02744de1cbc4ca06480a52-im-33,33,33-FF,FF,FF.gif) oznacza tę wartość dla
oznacza tę wartość dla 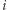 -elementowego prefiksu, czyli
-elementowego prefiksu, czyli 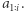 Wyniki będziemy wyznaczali w kolejności rosnącej długości prefiksów. Oczywiście
Wyniki będziemy wyznaczali w kolejności rosnącej długości prefiksów. Oczywiście ![|P1[i] = 1](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/6x-edc0a1341bd2106f6e02744de1cbc4ca06480a52-im-33,33,33-FF,FF,FF.gif) (mamy tylko jeden element). Zastanówmy się teraz, jak wyznaczyć
(mamy tylko jeden element). Zastanówmy się teraz, jak wyznaczyć ![P 1[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/7x-edc0a1341bd2106f6e02744de1cbc4ca06480a52-im-33,33,33-FF,FF,FF.gif) dla
dla 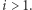 Jeśli
Jeśli 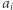 występowało wcześniej, wtedy
występowało wcześniej, wtedy ![|P1[i] = P1[i− 1].](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/10x-edc0a1341bd2106f6e02744de1cbc4ca06480a52-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku
W przeciwnym przypadku ![|P1[i] = P1[i− 1]+ 1.](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/11x-edc0a1341bd2106f6e02744de1cbc4ca06480a52-im-33,33,33-FF,FF,FF.gif) Do sprawdzania, czy
Do sprawdzania, czy 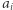 występowało wcześniej, możemy wykorzystać tablicę zliczającą.
występowało wcześniej, możemy wykorzystać tablicę zliczającą.
Przejdźmy teraz do obliczenia  Podobnie jak wcześniej, wartości tej tablicy będziemy obliczali od najkrótszych do najdłuższych prefiksów. Dodatkowo niech
Podobnie jak wcześniej, wartości tej tablicy będziemy obliczali od najkrótszych do najdłuższych prefiksów. Dodatkowo niech ![pop[x]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/2x-c183355dbb9a11c62af555a1bcc31b3bd32c33e9-im-33,33,33-FF,FF,FF.gif) dla
dla 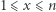 oznacza numer ostatniej pozycji spośród przejrzanych elementów, na której wystąpił
oznacza numer ostatniej pozycji spośród przejrzanych elementów, na której wystąpił 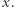
Najpierw dla jednoelementowego prefiksu ustawiamy ![P2[1] = 0](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/1x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) (nie ma podciągów dwuelementowych) oraz zapisujemy informację
(nie ma podciągów dwuelementowych) oraz zapisujemy informację ![pop[a ] = 1 1](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/2x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) (ostatnie wystąpienie wartości
(ostatnie wystąpienie wartości 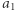 na pozycji numer 1). Następnie przeglądamy kolejne prefiksy. Załóżmy, że obliczamy
na pozycji numer 1). Następnie przeglądamy kolejne prefiksy. Załóżmy, że obliczamy ![P 2[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/4x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) dla
dla 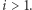 Otóż
Otóż ![P 2[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/6x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) to
to ![|P2[i− 1]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/7x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) powiększone o liczbę takich dwuelementowych podciągów
powiększone o liczbę takich dwuelementowych podciągów 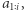 które nie występują w
które nie występują w 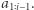 Szukane podciągi są postaci
Szukane podciągi są postaci 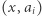 - drugi element ma wartość
- drugi element ma wartość 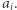 Wszystkich takich podciągów w
Wszystkich takich podciągów w 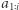 jest
jest ![|P1[i− 1],](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/13x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) gdyż na tyle sposobów można wybrać
gdyż na tyle sposobów można wybrać  Powinniśmy jednak odjąć te podciągi, które występują również w
Powinniśmy jednak odjąć te podciągi, które występują również w 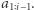 Jeśli
Jeśli 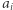 występuje pierwszy raz, wtedy nie musimy nic odejmować. Jeśli natomiast
występuje pierwszy raz, wtedy nie musimy nic odejmować. Jeśli natomiast 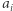 występowało wcześniej, to weźmy jego poprzednie wystąpienie na pozycji
występowało wcześniej, to weźmy jego poprzednie wystąpienie na pozycji ![|pop[ai].](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/18x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) Zauważmy, że jest ono drugim elementem
Zauważmy, że jest ono drugim elementem ![|P1[pop[ai]− 1]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/19x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) podciągów (na tyle sposobów można wybrać element stojący przed poprzednim wystąpieniem
podciągów (na tyle sposobów można wybrać element stojący przed poprzednim wystąpieniem 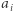 ). Zatem otrzymaliśmy, że:
). Zatem otrzymaliśmy, że: ![|P2[i] = P2[i −1]+ P 1[i −1]− P 1[pop[ai] − 1].](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/21x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) Po obliczeniu
Po obliczeniu ![P 2[i]](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/22x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) możemy zaktualizować
możemy zaktualizować ![pop[ai] = i.](/math/temat/informatyka/algorytmy/2020/03/29/theater-tickets/23x-67e050f4e9e64bc1724a72ac9e66d6ce09241eb1-im-33,33,33-FF,FF,FF.gif) Wyznaczyliśmy
Wyznaczyliśmy 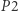 w czasie
w czasie 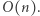 Druga faza algorytmu jest analogiczna do tej opisanej w sekcji Rozwiązanie
Druga faza algorytmu jest analogiczna do tej opisanej w sekcji Rozwiązanie 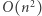 i działa w czasie
i działa w czasie 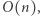 co daje nam pełne rozwiązanie o złożoności czasowej
co daje nam pełne rozwiązanie o złożoności czasowej